题目内容
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,
, ![]() 分别是它的左、右焦点,且存在直线
分别是它的左、右焦点,且存在直线![]() ,使
,使![]() 关于
关于![]() 的对称点恰好是圆
的对称点恰好是圆![]() (
(![]() )的一条直线的两个端点.
)的一条直线的两个端点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() (
(![]() )相交于
)相交于![]() 两点,射线
两点,射线![]() ,
, ![]() 与椭圆
与椭圆![]() 分别相交于点
分别相交于点![]() ,试探究:是否存在数集
,试探究:是否存在数集![]() ,当且仅当
,当且仅当![]() 时,总存在
时,总存在![]() ,使点
,使点![]() 在以线段
在以线段![]() 为直径的圆内?若存在,求出数集
为直径的圆内?若存在,求出数集![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由圆![]() 的方程配方得半径为2,由题设知,椭圆的焦距
的方程配方得半径为2,由题设知,椭圆的焦距![]() 等于圆
等于圆![]() 的直径,所以
的直径,所以![]() ,又
,又![]() ,可得椭圆方程.
,可得椭圆方程.
(2)由题可得直线![]() 是线段
是线段![]() 的垂直平分线,由
的垂直平分线,由![]() 方程与
方程与![]() ,联立可得:
,联立可得:
![]() ,
, ![]() .又点
.又点![]() 在以线段
在以线段![]() 为直径的圆内即
为直径的圆内即![]() ,
, ![]()
试题解析:(1)将圆![]() 的方程配方得:
的方程配方得: ![]() ,所以其圆心为
,所以其圆心为![]() ,半径为2,由题设知,椭圆的焦距
,半径为2,由题设知,椭圆的焦距![]() 等于圆
等于圆![]() 的直径,所以
的直径,所以![]() ,
,
又![]() ,所以
,所以![]() ,从而
,从而![]() ,故椭圆
,故椭圆![]() 的方程为
的方程为![]() .
.
(2)因为![]() 产于
产于![]() 的对称点恰好是圆
的对称点恰好是圆![]() 的一条直径的两个端点,所以直线
的一条直径的两个端点,所以直线![]() 是线段
是线段![]() 的垂直平分线(
的垂直平分线(![]() 是坐标原点),故
是坐标原点),故![]() 方程为
方程为![]() ,与
,与![]() ,联立得:
,联立得: ![]() ,由其判别式
,由其判别式![]() 得
得![]() ①.
①.
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
从而![]() ,
, 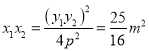 .
.
因为![]() 的坐标为
的坐标为![]() ,
,
所以![]() ,
, ![]() ,
,
注意到![]() 与
与![]() 同向,
同向, ![]() 与
与![]() 同向,所以
同向,所以
点![]() 在以线段
在以线段![]() 为直径的圆内
为直径的圆内![]() ,所以
,所以
![]() 即
即![]()
代入整理得![]() ②
②
当且仅当![]() 即
即![]() 时,总存在
时,总存在![]() ,使②成立.
,使②成立.
又当![]() 时,由韦达定理知方程
时,由韦达定理知方程![]() 的两根均为正数,故使②成立的
的两根均为正数,故使②成立的![]() ,从而满足①.
,从而满足①.
故存在数集![]() ,当且仅当
,当且仅当![]() 时,总存在
时,总存在![]() 使点
使点![]() 在以线段
在以线段![]() 为直径的圆内.
为直径的圆内.
点晴:本题主要考查直线与圆锥曲线位置关系. 直线和圆锥曲线的位置关系一方面要体现方程思想,另一方面要结合已知条件,从图形角度求解.联立直线与圆锥曲线的方程得到方程组,化为一元二次方程后由根与系数的关系求解是一个常用的方法. 涉及点![]() 在以线段
在以线段![]() 为直径的圆内
为直径的圆内![]() ,坐标化求解即可.
,坐标化求解即可.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】某小学为了解本校某年级女生的身高情况,从本校该年级的学生中随机选出100名女生并统计她们的身高(单位: ![]() ),得到如图频率分布表:
),得到如图频率分布表:
分组(身高) |
|
|
|
|
(Ⅰ)用分层抽样的方法从身高在![]() 和
和![]() 的女生中共抽取6人,则身高在
的女生中共抽取6人,则身高在![]() 的女生应抽取几人?
的女生应抽取几人?
(Ⅱ)在(Ⅰ)中抽取的6人中,再随机抽取2人,求这2人身高都在![]() 内的概率.
内的概率.
【题目】某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为
,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为![]() .
.

(Ⅰ)求![]() 的值,并求这50名同学心率的平均值;
的值,并求这50名同学心率的平均值;
(Ⅱ)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为0.8,请将下面的列联表补充完整,并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关?说明你的理由.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:  ,其中
,其中![]()
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计 | 50 |
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
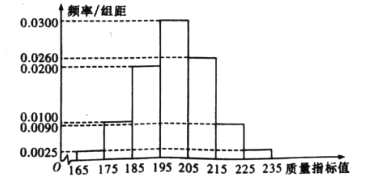
(1)根据以上抽样调查数据 ,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?