题目内容
【题目】数列{an}中，a1＝
，前n项和Sn满足Sn＋1－Sn＝(
)n＋1(n∈N*)．
(1)求数列{an}的通项公式an以及前n项和Sn；
(2)若S1，t(S1＋S2)，3(S2＋S3)成等差数列，求实数t的值．
【答案】(1)Sn＝
[1－(
)n](n∈N*)．
(2) t＝2.
【解析】试题分析：（1）由和项与通项关系得an＋1＝(
)n＋1再由a1＝
，得an＝(
)n，最后根据等比数列求和公式求Sn；（2）先根据（1）求S1，S2，S3再由S1，t(S1＋S2)，3(S2＋S3)成等差数列得2t(S1＋S2)= S1+3(S2＋S3)，代入解得实数t的值．
试题解析：解 (1)由Sn＋1－Sn＝(
)n＋1得an＋1＝()n＋1(n∈N*)，
又a1＝，故an＝()n(n∈N*)．
从而Sn＝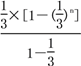
＝
[1－()n](n∈N*)．
(2)由(1)可得S1＝，S2＝
，S3＝
.
从而由S1，t(S1＋S2)，3(S2＋S3)成等差数列得
＋3×(＋)＝2×(＋)t，解得t＝2.
练习册系列答案
相关题目
