题目内容
8.如图所示,正弦曲线y=sinx,余弦曲线y=cosx与两直线x=0,x=π所围成的阴影部分的面积为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
分析 由图形可知,阴影部分的面积等于正弦函数与余弦函数图形$\frac{π}{4}$到$\frac{5}{4}π$的面积,所以利用此区间的定积分可求.
解答 解:由图形以及定积分的意义,得到所求封闭图形面积等价于$\int_{\frac{π}{4}}^{\frac{5π}{4}}{(sinx-cosx)dx}=\left.{(-cosx-sinx)}\right|_{\frac{π}{4}}^{\frac{5π}{4}}=2\sqrt{2}$;
故选:D.
点评 本小题主要考查定积分的几何意义以及定积分的基本运算,对学生的运算求解能力和数形结合思想提出一定要求.

练习册系列答案
相关题目
16.如图是秦九韶算法的一个程序框图,则输出的S为( )
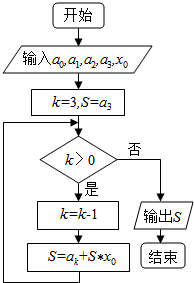

| A. | a1+x0(a3+x0(a0+a2x0))的值 | B. | a3+x0(a2+x0(a1+a0x0))的值 | ||
| C. | a0+x0(a1+x0(a2+a3x0))的值 | D. | a2+x0(a0+x0(a3+a1x0))的值 |
3.5名学生和2名老师排成一排照相,2名老师不在两边且不相邻的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
13.设a=sin42°,b=cos46°,c=2${\;}^{-\frac{1}{2}}$,则( )
| A. | c<a<b | B. | b<c<a | C. | a<b<c | D. | b<a<c |
18.执行下面的程序框图,那么输出的S等于( )
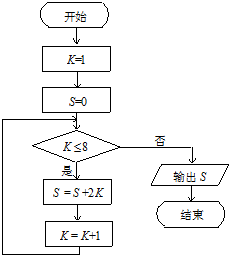

| A. | 42 | B. | 56 | C. | 72 | D. | 90 |
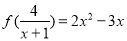 ,则
,则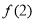 等于( )
等于( )