Question

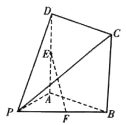
【题目】如图，四棱柱的底面为菱形，且.

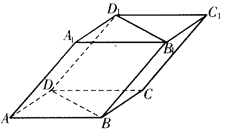
（1）证明：四边形为矩形；

（2）若，与平面所成的角为，求二面角的余弦值.

Answer 1

【答案】(1)见解析(2)

【解析】试题分析：(1)由四棱柱性质可知四边形 为平行四边形，连接，设，连接.，易证∴平面，∴.∵，∴； (2) 过点作平面，垂足为，由已知可得点在上，证明点与点重合，则平面，以为坐标原点，建立空间直角坐标系求出平面与平面的法向量，代入公式计算即可.

试题解析：

（1）证明:连接，设，连接.

∵，∴.

又为的中点，∴..

∴平面，∴.

∵，∴.

又四边形是平行四边形，则四边形为矩形.

（2）解:过点作平面，垂足为，由已知可得点在上，∴.

设，则.

在菱形中，，∴.

∴点与点重合，则平面.

以为坐标原点，建立空间直角坐标系.

则.

∴.

设平面的法向量为，则 ,∴即

取，可得为平面的一个法向量.

同理可得平面的一个法向量为。

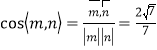∵.所以二面角的余弦值为.