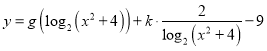题目内容
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=nan+n,数列{bn}的前n项和为Tn,求满足不等式![]() 的n的最小值.
的n的最小值.
【答案】(1)![]() ,n∈N*;(2)11
,n∈N*;(2)11
【解析】
(1)易求得![]() =1,由题意
=1,由题意![]() ,所以
,所以![]() ,两个式子做差变形可得递推关系式。根据等比数列的定义可得结论,利用等比数列通项公式可求得an。(2)bn是一个等比数列与一个等差数列相乘的形式,利用错位相减可求得其前n项和。再通过构造新数列以及其增减性得出满足不等式的最小n值。
,两个式子做差变形可得递推关系式。根据等比数列的定义可得结论,利用等比数列通项公式可求得an。(2)bn是一个等比数列与一个等差数列相乘的形式,利用错位相减可求得其前n项和。再通过构造新数列以及其增减性得出满足不等式的最小n值。
(1)证明:当n=1时,a1+1=2a1,∴a1=1.∵Sn+n=2an,n∈N*,
∴当n≥2时,Sn-1+n-1=2an-1,两式相减得:an+1=2an-2an-1,即an=2an-1+1,
∴an+1=2(an-1+1),∴数列{an+1}为以2为首项,2为公比的等比数列,
∴![]() ,则
,则![]() ,n∈N*;
,n∈N*;
(2)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
两式相减得:![]() ,
,
∴![]() ,由
,由![]() ,得
,得![]() ,
,
设![]() ,∵
,∵![]() >0,∴数列{cn}为递增数列,
>0,∴数列{cn}为递增数列,
∵![]() ,
,![]() ,
,
∴满足不等式![]() 的n的最小值为11.
的n的最小值为11.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目