题目内容
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,点
,点![]() 为短轴的一个端点,
为短轴的一个端点, ![]() ,若点
,若点![]() 在椭圆
在椭圆![]() 上,则点
上,则点![]() 称为点
称为点![]() 的一个“椭点”.
的一个“椭点”.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() 两点的“椭点”分别为
两点的“椭点”分别为![]() ,以
,以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,试求
,试求![]() 的面积.
的面积.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由已知得![]() ,又
,又![]() ,即可得方程;
,即可得方程;
(2)设![]() ,则
,则![]() ,由以
,由以![]() 为直径的圆经过坐标原点,得
为直径的圆经过坐标原点,得![]() ,即
,即![]() ,由
,由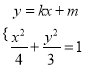 ,消除
,消除![]() 整理得:
整理得: ![]() ,结合韦达定理可得
,结合韦达定理可得![]() ,
, 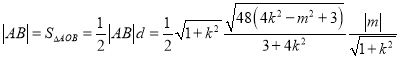 ,讲条件带入求解即可.
,讲条件带入求解即可.
试题解析:
(Ⅰ)由已知得![]() ,又
,又![]()
![]() ,
,
所以椭圆![]() 的方程为:
的方程为: ![]() ;
;
(Ⅱ)设![]() ,则
,则![]() ,
,
由以![]() 为直径的圆经过坐标原点,得
为直径的圆经过坐标原点,得![]() ,
,
即![]() (1)
(1)
由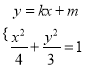 ,消除
,消除![]() 整理得:
整理得: ![]() ,
,
由![]() ,得
,得![]() ,
,
而![]() (2)
(2)
![]() (3)
(3)
将(2)(3)代入(1)得: 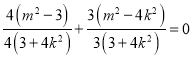 ,
,
即![]() ,
,
又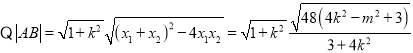 ,
,
原点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
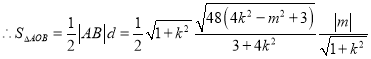 ,
,
把![]() 代入上式得
代入上式得![]() ,即
,即![]() 的面积是为
的面积是为![]() .
.

练习册系列答案
相关题目