题目内容
在数列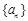 中,如果对任意的
中,如果对任意的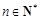 ,都有
,都有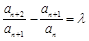 (
(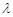 为常数),则称数列
为常数),则称数列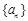 为比等差数列,
为比等差数列,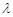 称为比公差.现给出以下命题:①若数列
称为比公差.现给出以下命题:①若数列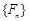 满足
满足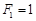 ,
,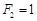 ,
,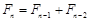 (
(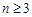 ),则该数列不是比等差数列;②若数列
),则该数列不是比等差数列;②若数列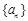 满足
满足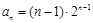 ,则数列
,则数列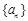 是比等差数列,且比公差
是比等差数列,且比公差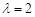 ;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若
;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若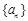 是等差数列,
是等差数列,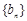 是等比数列,则数列
是等比数列,则数列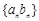 是比等差数列.
是比等差数列.
其中所有真命题的序号是_________________.
①③
解析试题分析:根据新定义可知:①若数列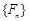 满足
满足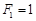 ,
,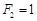 ,
,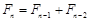 (
(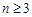 ),则该数列不是比等差数列:因为
),则该数列不是比等差数列:因为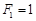 ,
,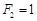 ,
,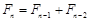 ,所以
,所以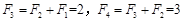 ,所以
,所以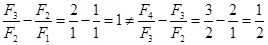 ,所以不成立。
,所以不成立。
②若数列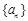 满足
满足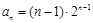 ,则数列
,则数列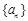 是比等差数列,且比公差
是比等差数列,且比公差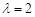 :因为
:因为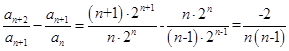 不是常数,所以不成立;
不是常数,所以不成立;
③等比数列一定是比等差数列,等差数列不一定是比等差数列:若数列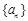 是等比数列,则
是等比数列,则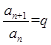 ,所以
,所以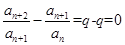 ,所以是比等差数列,成立;
,所以是比等差数列,成立;
④若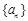 是等差数列,
是等差数列,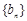 是等比数列,则数列
是等比数列,则数列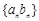 是比等差数列:当
是比等差数列:当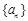 和
和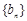 是非0常数列时,成立,其他的不一定成立。
是非0常数列时,成立,其他的不一定成立。
考点:数列的应用。
点评:本题考查新定义的理解和运算,解决该试题的关键是应正确理解新定义,并结合所学知识来判定,同时注意利用列举法判断命题为假

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 .
.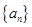 ,如果
,如果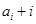 (
(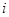 =1,2,3, )为完全平方数,则称数列
=1,2,3, )为完全平方数,则称数列 性质”;不论数列
性质”;不论数列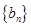 与
与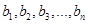 是
是 的一个排列;
的一个排列; 项和
项和 ;
;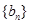 :1,2,3,4,5;
:1,2,3,4,5;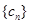 :1,2,3,4,5,6,7,8,9,10,11.
:1,2,3,4,5,6,7,8,9,10,11.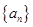 中,
中,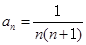 ,其前n项的和是
,其前n项的和是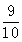 ,则在平面直角坐标系中,直线
,则在平面直角坐标系中,直线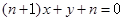 在y轴上的截距为 。
在y轴上的截距为 。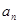 }的前n项和为
}的前n项和为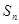 ,
,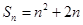 ,则
,则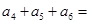 。
。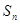 是数列
是数列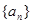 的前
的前 项和,向量
项和,向量 ,
,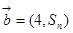 ,且满足
,且满足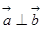 ,则
,则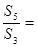
 的前n项和记为
的前n项和记为 ,点(n,
,点(n,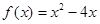 (
(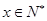 )上
)上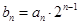 ,求数列
,求数列 的前n项和
的前n项和 的值.
的值. 的前
的前 项和为
项和为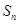 ,
,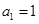 ,
,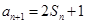 ,等差数列
,等差数列 满足
满足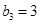 ,
,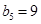 .
.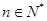 ,不等式
,不等式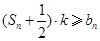 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.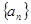 满足:
满足: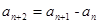 (
(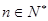 ),且
),且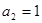 ,若数列的前2011项之
,若数列的前2011项之