题目内容
已知 ,则直线
,则直线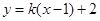 被圆
被圆 截得的弦长的最小值为
截得的弦长的最小值为
 ,则直线
,则直线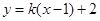 被圆
被圆 截得的弦长的最小值为
截得的弦长的最小值为A. | B. | C.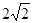 | D.2 |
D
圆 的方程可化为
的方程可化为 ,此为圆心为
,此为圆心为 ,半径为
,半径为 的圆;
的圆;
直线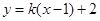 恒过点
恒过点 ,且此
,且此 点在圆内,由垂径定理可知,当圆心
点在圆内,由垂径定理可知,当圆心 与点
与点 的连线垂直于直线
的连线垂直于直线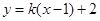 时,截得的弦长最小.此时
时,截得的弦长最小.此时 恰为弦的中点.
恰为弦的中点.
由两点间的距离公式有 ,在三角形中,由勾股定理得
,在三角形中,由勾股定理得

 的方程可化为
的方程可化为 ,此为圆心为
,此为圆心为 ,半径为
,半径为 的圆;
的圆;直线
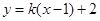 恒过点
恒过点 ,且此
,且此 点在圆内,由垂径定理可知,当圆心
点在圆内,由垂径定理可知,当圆心 与点
与点 的连线垂直于直线
的连线垂直于直线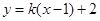 时,截得的弦长最小.此时
时,截得的弦长最小.此时 恰为弦的中点.
恰为弦的中点.由两点间的距离公式有
 ,在三角形中,由勾股定理得
,在三角形中,由勾股定理得


练习册系列答案
相关题目
 与
与 轴相切,且圆
轴相切,且圆 上,求圆
上,求圆 与
与 轴相切,圆心
轴相切,圆心 上,且截直
上,且截直 的弦长为2
的弦长为2 ,求圆
,求圆 的方程。
的方程。 过圆
过圆 的圆心,则a的值为
的圆心,则a的值为 1
1 ,圆心在直线y=2x上,圆M被直线x-y=0截得的弦长为
,圆心在直线y=2x上,圆M被直线x-y=0截得的弦长为 ,求圆M的方程
,求圆M的方程
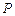 ,则点
,则点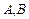 距离之和的最大值为 ▲ .
距离之和的最大值为 ▲ . 1);
1);