题目内容
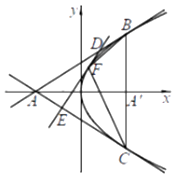
【题目】如图，在△ABC中，sin 
= 
，AB=2，点D在线段AC上，且AD=2DC，BD= 
，则cosC= ． 
【答案】
【解析】解：因为sin 
= 
，所以cos∠ABC=1﹣2sin2 =1﹣2×（ ）2=1﹣2× 
= ，
在△ABC中，设BC=a，AC=3b，
由余弦定理可得 
：①
在△ABD和△DBC中，由余弦定理可得：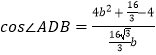 
，
，
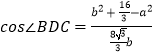因为cos∠ADB=﹣cos∠BDC，所以有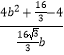 
= 
，
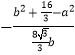所以3b2﹣a2=﹣6 ②
由①②可得a=3，b=1，即BC=3，AC=3．
则cosC= 
= 
，
所以答案是： 
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识，掌握正弦定理:
，以及对余弦定理的定义的理解，了解余弦定理:
;
;
．
练习册系列答案
相关题目
