题目内容
【题目】已知函数f(x)=|x+a|+|x+ ![]() |(a>0)
|(a>0)
(1)当a=2时,求不等式f(x)>3的解集;
(2)证明:f(m)+f(﹣ ![]() )≥4.
)≥4.
【答案】
(1)解:当a=2时,求不等式f(x)>3,即|x+2|+|x+ ![]() |>3.
|>3.
而|x+2|+|x+ ![]() |表示数轴上的x对应点到﹣2、﹣
|表示数轴上的x对应点到﹣2、﹣ ![]() 对应点的距离之和,
对应点的距离之和,
而0和﹣3对应点到﹣ ![]() 、
、 ![]() 对应点的距离之和正好等于3,
对应点的距离之和正好等于3,
故不等式f(x)>3的解集为{x|x<﹣ ![]() ,或 x>
,或 x> ![]() }.
}.
(2)证明:∵f(m)+f(﹣ ![]() )=|m+a|+|m+
)=|m+a|+|m+ ![]() |+|﹣
|+|﹣ ![]() +a||﹣
+a||﹣ ![]() +
+ ![]() |
|
=(|m+a|+|﹣ ![]() +a|)+(|m+
+a|)+(|m+ ![]() |+|﹣
|+|﹣ ![]() +
+ ![]() |)≥2(|m+
|)≥2(|m+ ![]() |)=2(|m|+|
|)=2(|m|+| ![]() |)≥4,
|)≥4,
∴原结论成立.
【解析】(1)当a=2时,求不等式即|x+2|+|x+ ![]() |>3,再利用对值的意义求得它的解集.(2)由条件利用绝对值三角不等式、基本不等式,证得要证的结论.
|>3,再利用对值的意义求得它的解集.(2)由条件利用绝对值三角不等式、基本不等式,证得要证的结论.
【考点精析】通过灵活运用绝对值不等式的解法,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号即可以解答此题.

【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图: 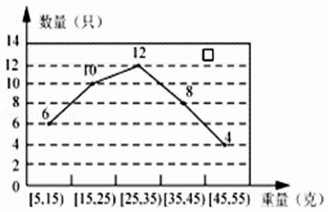
(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) | [5,25) | [25,45) | [45,55] |
按分层抽样抽取10只,再随机抽取3只品尝,记X为抽到二等品的数量,求抽到二级品的期望.
【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米. 
(1)完成2×2列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
(2)为了改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,选取的植株均为矮茎的概率是多少?


