题目内容
【题目】给出下列五个命题,其中正确的命题序号是________.
①当![]() 时,函数
时,函数![]() 取得最大值,则
取得最大值,则![]()
②已知菱形![]() ,
,![]() 为
为![]() 的中点,且
的中点,且![]() ,则菱形
,则菱形![]() 面积的最大值为12
面积的最大值为12
③已知二次函数![]() ,如果
,如果![]() 时
时![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]()
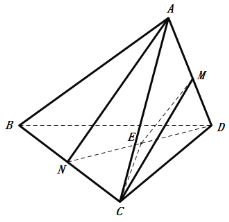
④在三棱锥![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,则异面直线
的中点,则异面直线![]() 所成的角的余弦值是
所成的角的余弦值是![]()
⑤数列![]() 满足
满足![]() ,且数列
,且数列![]() 的前2010项的和为403,记数列
的前2010项的和为403,记数列![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,则
项和,则![]()
【答案】②③
【解析】
根据三角函数最值,面积的最值,不等式恒成立,求异面直线夹角,数列求和的方法依次判断每个选项得到答案.
①![]() ,其中
,其中![]() .
.
取得最大值时:![]() ,则
,则![]() ,①错误;
,①错误;
②设![]() ,菱形边长为
,菱形边长为![]() ,则
,则![]() ,即
,即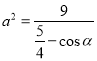 .
.
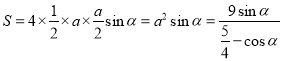 ,
,
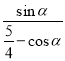 表示的单位圆上的点
表示的单位圆上的点![]() 到
到![]() 的斜率,
的斜率,
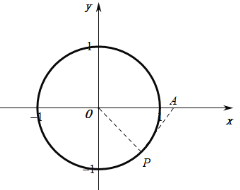
如图所示:当直线![]() 与圆相切时斜率有最大值为
与圆相切时斜率有最大值为![]() ,故
,故![]() ,故②正确;
,故②正确;
③已知二次函数![]() ,
,![]() 时
时![]() ,即
,即![]() 恒成立.
恒成立.
当![]() 时,成立;
时,成立;
当![]() 时,
时,![]() ,即
,即![]() .
.
故![]() ,③正确;
,③正确;
④如图所示:连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,![]() 为异面直线
为异面直线![]() 所成的角,计算得到
所成的角,计算得到![]() ,
,![]() ,
,![]() .
.
利用余弦定理得到:![]() ,故④错误;
,故④错误;
⑤![]() ,设
,设![]() ,则
,则![]() ,
,![]() .
.
故数列周期为![]() ,
,![]() ,
,![]() ,故⑤错误;
,故⑤错误;
故答案为:②③.

练习册系列答案
相关题目

