题目内容
【题目】若函数
在
处有极大值，则常数
为（ ）
A.2或6B.2C.6D.-2或-6
【答案】C
【解析】
先求导，再解
，得到c=6或 c=2，再检验得到常数c的值.
∵函数f（x）=x（x﹣c）2=x3﹣2cx2+c2x，它的导数为
=3x2﹣4cx+c2，
由题意知在x=2处的导数值为 12﹣8c+c2=0，∴c=6或 c=2，
又函数f（x）=x（x﹣c）2在x=2处有极大值，
故导数值在x=2处左侧为正数，右侧为负数．
当c=2时，=3x2﹣8x+4=3（x﹣
）（x﹣2），
不满足导数值在x=2处左侧为正数，右侧为负数．
当c=6时，=3x2﹣24x+36=3（x2﹣8x+12）=3（x﹣2）（x﹣6），
满足导数值在x=2处左侧为正数，右侧为负数．故 c=6．
故答案为：C
练习册系列答案
阅读快车系列答案
相关题目
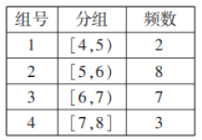
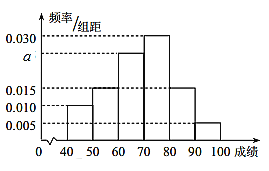
【题目】在某校举行的航天知识竞赛中，参与竞赛文科生与理科生人数之比为
，且成绩分布在
，分数在80以上（含80）的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本，得到成绩的频率分布直方图如图所示.
文科生 | 理科生 | 合计 | |
获奖 | 5 | ||
不获奖 | |||
合计 | 200 |
参考公式：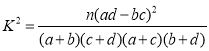
（其中
为样本容量）
随机变量
的概率分布：
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 | |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（1）求
的值；
（2）填写上方的
列联表，并判断能否有超过
的把握认为“获奖与学生的文、理科有关”?
