题目内容
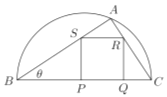
【题目】校园准备绿化一块直径为![]() 的半圆形空地,点
的半圆形空地,点![]() 在半圆圆弧上,△
在半圆圆弧上,△![]() 外的地方种草,△
外的地方种草,△![]() 的内接正方形
的内接正方形![]() 为一水池(
为一水池(![]() ,
,![]() 在
在![]() 边上),其余地方种花,若
边上),其余地方种花,若![]() ,
, ![]() ,设△
,设△![]() 的面积为
的面积为![]() ,正方形面积为
,正方形面积为![]() ;
;
(1)用![]() 和
和![]() 表示
表示![]() 和
和![]() ;
;
(2)当![]() 固定,
固定,![]() 变化时,求
变化时,求![]() 最小值及此时的角
最小值及此时的角![]() ;
;
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() 最小值为
最小值为![]() ,此时
,此时![]() ;
;
【解析】
(1)据题知三角形![]() 为直角三角形,根据三角函数分别求出AC和AB,求出三角形ABC的面积
为直角三角形,根据三角函数分别求出AC和AB,求出三角形ABC的面积![]() ;设正方形
;设正方形![]() 的边长为
的边长为![]() ,利用三角函数分别表示出BS和AS,利用
,利用三角函数分别表示出BS和AS,利用![]() 列出方程求出
列出方程求出![]() ,算出
,算出![]() ;
;
(2)可设![]() 来化简求出
来化简求出![]() 与
与![]() 的比值,利用对勾函数的增减性求出比值的最小值即可求出此时的
的比值,利用对勾函数的增减性求出比值的最小值即可求出此时的![]() .
.
解:(1)在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,
设正方形的边长为![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,故
,故![]() ,
,
所以![]() ,
,![]() ;
;
(2)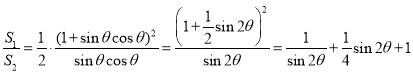 ,
,
令![]() ,因为
,因为![]() ,
,
所以![]() ,则
,则![]() ,
,
所以![]() ,
,
由对勾函数的单调性得:函数![]() 在
在![]() 上递减,
上递减,
因此当![]() 时
时![]() 有最小值
有最小值![]() ,
,
此时![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() 最小,最小值为
最小,最小值为![]() .
.

练习册系列答案
相关题目
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为n的样本,得到一周参加社区服务的时间的统计数据如下表:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(1)求m,n;
(2)能否有95多的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(3)以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,现从该校学生中随机调查6名学生,试估计6名学生中一周参加社区服务时间超过1小时的人数.
附:
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |