题目内容
已知点是F抛物线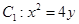 与椭圆
与椭圆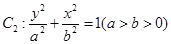 的公共焦点,且椭圆的离心率为
的公共焦点,且椭圆的离心率为

(1)求椭圆的方程;
(2)过抛物线上一点P,作抛物线的切线 ,切点P在第一象限,如图,设切线
,切点P在第一象限,如图,设切线 与椭圆相交于不同的两点A、B,记直线OP,FA,FB的斜率分别为
与椭圆相交于不同的两点A、B,记直线OP,FA,FB的斜率分别为 (其中
(其中 为坐标原点),若
为坐标原点),若 ,求点P的坐标.
,求点P的坐标.
(1)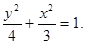 (2)
(2)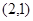 .
.
解析试题分析:(1)因为点F的坐标为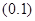 ,则有
,则有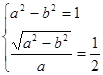 ,
,
从而有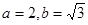 ,故椭圆方程为
,故椭圆方程为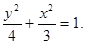 4分
4分
(2)设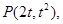 由
由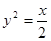 ,得切线的斜率为
,得切线的斜率为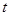 ,从而切线
,从而切线 的方程为:
的方程为: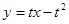 ,
,
由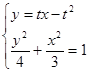 ,得
,得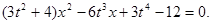
设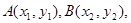 则有
则有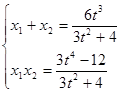 ,
,
而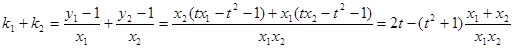
从而有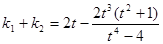 ,又
,又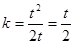 ,
,
则有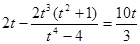 ,而
,而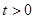 ,故有
,故有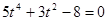 ,
,
得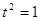 ,故
,故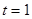 ,即得点P的坐标为
,即得点P的坐标为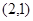 . 10分
. 10分
考点:本题考查了椭圆的方程及直线与椭圆的位置关系
点评:对于直线与圆锥曲线的综合问题,往往要联立方程,同时结合一元二次方程根与系数的关系进行求解;而对于最值问题,则可将该表达式用直线斜率k表示,然后根据题意将其进行化简结合表达式的形式选取最值的计算方式

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
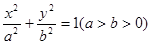 的两个焦点为F1、F2,点P在椭圆C上,且|PF1|=
的两个焦点为F1、F2,点P在椭圆C上,且|PF1|=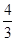 ,
,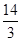 , PF1⊥F1F2.
, PF1⊥F1F2.  (α为参数).
(α为参数).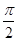 ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;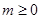 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量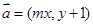 ,向量
,向量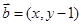 ,
, ,动点
,动点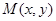 的轨迹为E.
的轨迹为E.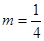 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且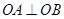 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程; 与圆C:
与圆C: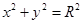 (1<R<2)相切于A1,且
(1<R<2)相切于A1,且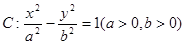 的两个焦点为
的两个焦点为 的曲线C上.(Ⅰ)求双曲线C的方程;
的曲线C上.(Ⅰ)求双曲线C的方程;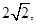 求直线l的方程
求直线l的方程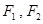 为椭圆
为椭圆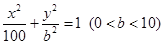 的左、右焦点,
的左、右焦点,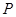 是椭圆上一点,若
是椭圆上一点,若 。
。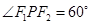 求
求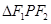 的面积。
的面积。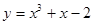 在点
在点 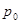 处的切线
处的切线 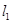 平行直线
平行直线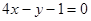 ,且点
,且点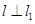 , 且
, 且 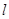 也过切点
也过切点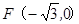 ,且过点
,且过点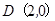 .
.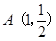 ,若
,若 是椭圆上的动点,求线段
是椭圆上的动点,求线段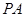 的中点
的中点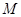 的轨迹方程.
的轨迹方程.  ,椭圆
,椭圆 以
以 的长轴为短轴,且与
的长轴为短轴,且与 ,求直线
,求直线 的方程.
的方程.