题目内容
【题目】已知
为抛物线
上一个动点， 
为圆
上一个动点，那么点
到点
的距离与点
到抛物线的准线距离之和的最小值是（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】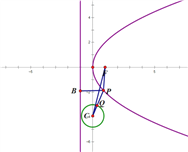
由已知得，设圆心为
，因为圆
， 
抛物线
上一动点， 
为抛物线的焦点
的最短距离为
， 
，则当
的直线经过点
时， 
最小，则
，故选A.
【方法点晴】本题主要考查抛物线的标准方程和抛物线的简单性质及利用抛物线的定义求最值，属于难题.与抛物线的定义有关的最值问题常常实现由点到点的距离与点到直线的距离的转化：(1)将抛物线上的点到准线的距化为该点到焦点的距离，构造出“两点之间线段最短”，使问题得解；(2)将拋物线上的点到焦点的距离转化为到准线的距离，利用“点与直线上所有点的连线中垂线段最短”原理解决.本题是将
到准线的距离转化为到焦点的距离，再根据几何意义解题的.
练习册系列答案
相关题目
【题目】2017年1月1日，作为贵阳市打造“千园之城”27个示范性公园之一的泉湖公园正式开园.元旦期间，为了活跃气氛，主办方设置了水上挑战项目向全体市民开放.现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查，统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况，具体数据如图表：
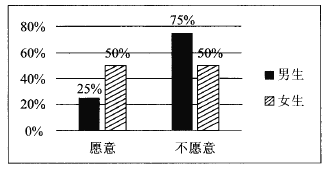
（1）根据条件完成下列
列联表，并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关？
愿意 | 不愿意 | 总计 | |
男生 | |||
女生 | |||
总计 |
（2）现用分层抽样的方法从愿意接受挑战的市民中选取7名挑战者，再从中抽取2人参加挑战，求抽取的2人中至少有一名男生的概率.
参考数据及公式：
| 0.1 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
.
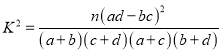