题目内容
【题目】四棱锥P-ABCD的底面ABCD是正方形,E,F分别为AC和PB上的点,它的直观图,正视图,侧视图如图所示.
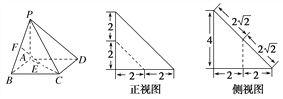
(1)求EF与平面ABCD所成角的大小;
(2)求二面角B-PA-C的大小.
【答案】(1)45°;(2)45°
【解析】试题分析:(1)取AB中点G,连接FG,GE,则FG∥PA,GE∥BC,可得D,∠FEG为EF与平面ABCD所成的角,解三角形可求;(2)由PA⊥BA,PA⊥CA,知∠BAC为二面角B-PA-C的平面角,即可求解.
试题解析:
根据三视图可知:PA垂直于平面ABCD,点E,F分别为AC和PB的中点,ABCD是边长为4的正方形,且PA=4.
(1)如图,取AB中点G,连接FG,GE,则FG∥PA,GE∥BC,所以FG⊥平面ABCD,∠FEG为EF与平面ABCD所成的角,在Rt△FGE中,FG=2,GE=2,所以∠FEG=45°.
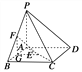
(2)因为PA⊥平面ABCD,所以PA⊥BA,PA⊥CA,
所以∠BAC为二面角B-PA-C的平面角.
又因为∠BAC=45°,
所以二面角B-AP-C的平面角的大小为45°.

【题目】2017年1月1日,作为贵阳市打造“千园之城”27个示范性公园之一的泉湖公园正式开园.元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放.现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
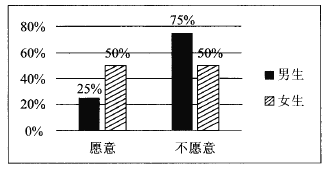
(1)根据条件完成下列![]() 列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
愿意 | 不愿意 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)现用分层抽样的方法从愿意接受挑战的市民中选取7名挑战者,再从中抽取2人参加挑战,求抽取的2人中至少有一名男生的概率.
参考数据及公式:
| 0.1 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
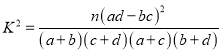 .
.
【题目】网络购物已经成为一种时尚,电商们为了提升知名度,加大了在媒体上的广告投入.经统计,近五年某电商在媒体上的广告投入费用x(亿元)与当年度该电商的销售收入y(亿元)的数据如下表:):
年份 | 2012年 | 2013年 | 2014 | 2015 | 2016 |
广告投入x | 0.8 | 0.9 | 1 | 1.1 | 1.2 |
销售收入y | 16 | 23 | 25 | 26 | 30 |
(1)求y关于x的回归方程; (2)2017年度该电商准备投入广告费1.5亿元,
利用(1)中的回归方程,预测该电商2017年的销售收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: 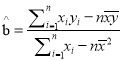
![]() ,选用数据:
,选用数据: ![]() ,
, ![]()
