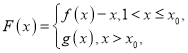题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)记![]() 表示
表示![]() 中的最小值,设
中的最小值,设![]() ,若函数
,若函数![]() 至少有三个零点,求实数
至少有三个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单减区间为![]() 和
和![]() ,单增区间为
,单增区间为![]() .(2)
.(2)![]()
【解析】
(1)求出![]() ,由
,由![]() 得
得![]() ,
,![]() ,讨论两根大小,得出
,讨论两根大小,得出![]() 的正负,从而确定单调区间;
的正负,从而确定单调区间;
(2)![]() 只有唯一零点2,因此
只有唯一零点2,因此![]() 在
在![]() 上至少有两个零点才能满足题意,根据(1)中得出的单调性,分类讨论
上至少有两个零点才能满足题意,根据(1)中得出的单调性,分类讨论![]() 的极值与零点可得.
的极值与零点可得.
(1)![]() 的定义域为
的定义域为![]() ,
,
∴![]() ,令
,令![]() ,得
,得![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() ;
;
②当![]() ,即
,即![]() 时,
时,![]() ;
;
③当![]() ,即
,即![]() 时,
时,![]() ,
,
综上,当![]() 时,
时,![]() 的单减区间为
的单减区间为![]() 和
和![]() ,单增区间为
,单增区间为![]() ;当
;当![]() 时,
时,![]() 的单减区间为
的单减区间为![]() ,无增区间;当
,无增区间;当![]() 时,
时,![]() 的单减区间为
的单减区间为![]() 和
和![]() ,单增区间为
,单增区间为![]() .
.
(2)![]() 的唯一一个零点是
的唯一一个零点是![]() ,∴
,∴![]() ,由(1)可得: (i)当
,由(1)可得: (i)当![]() 时,
时,![]() ,此时
,此时![]() 至多有两个零点,不符合题意;(ii)当
至多有两个零点,不符合题意;(ii)当![]() 时,
时,![]() 在定义域
在定义域![]() 上单减递减,此时
上单减递减,此时![]() 至多有两个零点,不符合题意; (ⅲ)当
至多有两个零点,不符合题意; (ⅲ)当![]() 时,若
时,若![]() ,即
,即![]() ,此时
,此时![]() 至多有两个零点,不符合题意;若
至多有两个零点,不符合题意;若![]() ,即
,即![]() ,此时
,此时![]() ,即
,即![]() ,此时
,此时![]() 恰好有三个零点,符合题意;若
恰好有三个零点,符合题意;若![]() ,即
,即![]() ,此时
,此时![]() ,
, ![]() ,记
,记![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,此时
,此时![]() 恰好有四个零点,符合题意,综上,
恰好有四个零点,符合题意,综上,![]() .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
【题目】某校高一年级有甲,乙,丙三位学生,他们前三次月考的物理成绩如表:
第一次月考物理成绩 | 第二次月考物理成绩 | 第三次月考物理成绩 | |
学生甲 | 80 | 85 | 90 |
学生乙 | 81 | 83 | 85 |
学生丙 | 90 | 86 | 82 |
则下列结论正确的是( )
A. 甲,乙,丙第三次月考物理成绩的平均数为86
B. 在这三次月考物理成绩中,甲的成绩平均分最高
C. 在这三次月考物理成绩中,乙的成绩最稳定
D. 在这三次月考物理成绩中,丙的成绩方差最大