题目内容
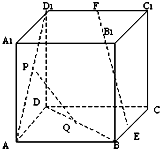 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.(1)求证:PQ∥平面DCC1D1;
(2)求EF的长,并求异面直线PQ,EF所成角的余弦值.
分析:(1)连接AC,CD1,由P,Q分别为AD1、AC的中点,知PQ∥CD1,由此能够证明PQ∥平面DCC1D1.
(2)建立空间直角坐标系,求出E、F、P、Q,坐标利用空间两点距离公式直接求EF的长,利用向量数量积求异面直线PQ,EF所成角的余弦值.
(2)建立空间直角坐标系,求出E、F、P、Q,坐标利用空间两点距离公式直接求EF的长,利用向量数量积求异面直线PQ,EF所成角的余弦值.
解答: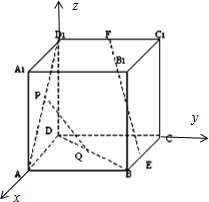 解:(1)证明:如图所示,连接AC,CD1,
解:(1)证明:如图所示,连接AC,CD1,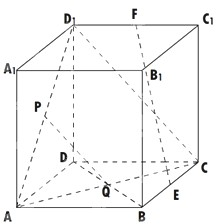
∵P,Q分别为AD1、AC的中点,∴PQ∥CD1,
∵CD1?平面DCC1D1,PQ?平面DCC1D1,
∴PQ∥平面DCC1D1.
(2)建立如图所示的空间直角坐标系,因为正方体的棱长为a,所以D(0,0,0),E(
,a,0),F(0,
,a),P(
,0,
),Q(
,
,0),
所以
=(-
,
,a).
=(0,-
,
),
所以EF的长:|
|=
=
a.
异面直线PQ,EF所成角的余弦值:cosθ=
=
=
.
 解:(1)证明:如图所示,连接AC,CD1,
解:(1)证明:如图所示,连接AC,CD1,
∵P,Q分别为AD1、AC的中点,∴PQ∥CD1,
∵CD1?平面DCC1D1,PQ?平面DCC1D1,
∴PQ∥平面DCC1D1.
(2)建立如图所示的空间直角坐标系,因为正方体的棱长为a,所以D(0,0,0),E(
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
所以
| EF |
| a |
| 2 |
| a |
| 2 |
| QP |
| a |
| 2 |
| a |
| 2 |
所以EF的长:|
| EF |
(-
|
| ||
| 2 |
异面直线PQ,EF所成角的余弦值:cosθ=
| ||||
|
|
| ||||||||
|
| ||
| 6 |
点评:本题考查直线与平面平行的证明,考查异面直线所成角的求法,空间两点的距离公式.解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( ) ,当
,当 取什么位置时,三棱柱的体积最大?
取什么位置时,三棱柱的体积最大?





