题目内容
设函数f0(x)=1-x2,f1(x)=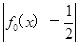 ,fn(x)=
,fn(x)=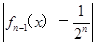 ,(n≥1,n≥N),则方程f1(x)=
,(n≥1,n≥N),则方程f1(x)=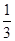 有________个实数根,方程fn(x)=
有________个实数根,方程fn(x)=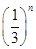 有________个实数根.
有________个实数根.
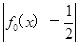 ,fn(x)=
,fn(x)=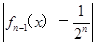 ,(n≥1,n≥N),则方程f1(x)=
,(n≥1,n≥N),则方程f1(x)=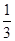 有________个实数根,方程fn(x)=
有________个实数根,方程fn(x)=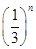 有________个实数根.
有________个实数根.4,2n+1
f1(x)=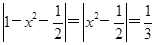 ,∴x2=
,∴x2=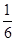 或x2=
或x2=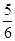 有4个解.
有4个解.
∵可推出n=1,2,3…,根个数分别为22,23,24,
∴通过类比得出fn(x)=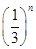 有2n+1个实数根.
有2n+1个实数根.
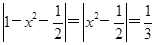 ,∴x2=
,∴x2=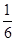 或x2=
或x2=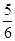 有4个解.
有4个解.∵可推出n=1,2,3…,根个数分别为22,23,24,
∴通过类比得出fn(x)=
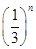 有2n+1个实数根.
有2n+1个实数根.
练习册系列答案
相关题目
 ,n∈N+,求a2,a3,a4
,n∈N+,求a2,a3,a4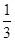 +
+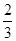 =
=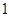 ;
;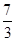 +
+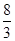 +
+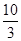 +
+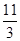 =
=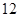 ;
;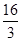 +
+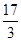 +
+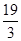 +
+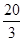 +
+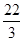 +
+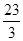 =
=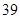 ;
;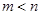 且
且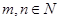 时,
时,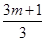 +
+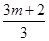 +
+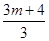 +
+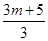 ++
++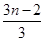 +
+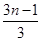 =________(最后结果用
=________(最后结果用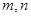 表示).
表示).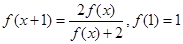
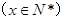 ,猜想
,猜想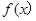 的表达式为
的表达式为  .将这个结论类比到空间:在三棱锥A-BCD中,平面DEC平分二面角A-CD-B且与AB交于E,则类比的结论为
.将这个结论类比到空间:在三棱锥A-BCD中,平面DEC平分二面角A-CD-B且与AB交于E,则类比的结论为 =________.
=________.
 行的从左至右的第
行的从左至右的第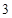 个数是 .
个数是 .