题目内容
在数列{an}中，a1＝1，an＋1＝
，n∈N＋，求a2，a3，a4
并猜想数列的通项公式，并给出证明．
，n∈N＋，求a2，a3，a4并猜想数列的通项公式，并给出证明．
an＝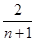
(n∈N＋)，证明见解析
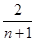(n∈N＋)，证明见解析{an}中a1＝1，a2＝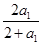
＝
，
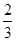a3＝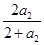
＝
＝
，
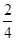a4＝
＝
，…，
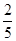所以猜想{an}的通项公式an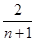＝ (n∈N＋)．此猜想正确．
证明如下：因为a1＝1，an＋1＝，
所以
＝
＝
＋，
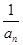即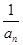－＝，所以数列
是以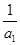
＝1为首项，
公差为的等差数列，
所以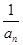＝1＋(n－1) ＝
＋，
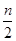即通项公式an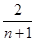＝ (n∈N＋)
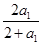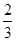＝，a3＝
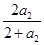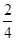＝＝，a4＝
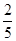＝，…，所以猜想{an}的通项公式an＝
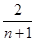(n∈N＋)．此猜想正确．证明如下：因为a1＝1，an＋1＝
，所以
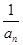＝＝＋，即
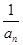－＝，所以数列是以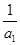＝1为首项，公差为
的等差数列，所以
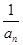＝1＋(n－1) 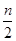＝＋，即通项公式an＝
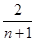(n∈N＋)
练习册系列答案
阅读快车系列答案
相关题目
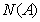为有限集合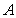
的某项指标，已知
，
，
，
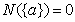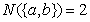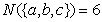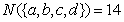，运用归纳推理，可猜想出的合理结论是：若
，
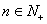（结果用含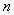
的式子表示）.
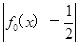，fn(x)＝
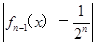，(n≥1，n≥N)，则方程f1(x)＝
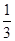有________个实数根，方程fn(x)＝
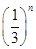有________个实数根．
＝1的面积S＝πab
(n2－1)[1－(－1)n]的值 ( )
,由此归纳出{an}的通项公式
．可得
；进而还可以算出
、
的值，并
.（
）