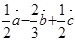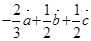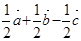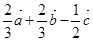题目内容
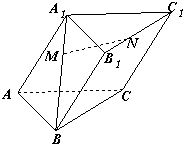
三棱柱ABC-A1B1C1中，M、N分别是A1B、B1C1上的点，且BM=2A1M，C1N=2B1N．设
=
，
=
，
=
．
（Ⅰ）试用
，
，
表示向量
；
（Ⅱ）若∠BAC=90°，∠BAA1=∠CAA1=60°，AB=AC=AA1=1，求MN的长．
| AB |
| a |
| AC |
| b |
| AA1 |
| c |
（Ⅰ）试用
| a |
| b |
| c |
| MN |
（Ⅱ）若∠BAC=90°，∠BAA1=∠CAA1=60°，AB=AC=AA1=1，求MN的长．
（Ⅰ）由图形知
=
+
+
=
+
+
=
(
-
)+
+
(
-
)=
+
+
．
（Ⅱ）由题设条件
∵(
+
+
)2=
2+
2+
2+2
•
+2
•
+2
•
=1+1+1+0+2×1×1×
+2×1×1×
=5，
∴|
+
+
|=
，|
|=
|
+
+
=|
．
| MN |
| MA1 |
| A1B1 |
| B1N |
| 1 |
| 3 |
| BA1 |
| AB |
| 1 |
| 3 |
| B1C1 |
| 1 |
| 3 |
| c |
| a |
| a |
| 1 |
| 3 |
| b |
| a |
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| 1 |
| 3 |
| c |
（Ⅱ）由题设条件
∵(
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| 1 |
| 2 |
| 1 |
| 2 |
∴|
| a |
| b |
| c |
| 5 |
| MN |
| 1 |
| 3 |
| a |
| b |
| c |
| ||
| 3 |
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
，
.
与
共线时，求
的值；
=(c-a)?(c-b)的最大值为 .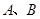
为空间的两个不同的点，且
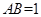，空间中适合条件
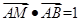的点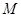
的集合表示的图形是 . 
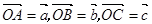，点M在OA上，且OM=2MA，N为BC中点，则
= （ ）
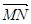