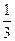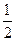题目内容
已知向量a=(1,-2),b=(4,2),c=(x,y).若|c|的取值范围是[0,5],则实数 =(c-a)?(c-b)的最大值为 .
=(c-a)?(c-b)的最大值为 .
 =(c-a)?(c-b)的最大值为 .
=(c-a)?(c-b)的最大值为 .0
∵ =(c-a)?(c-b)=(1-x,-2-y)?(4-x,2-y)=x2-5x+y2=(x-
=(c-a)?(c-b)=(1-x,-2-y)?(4-x,2-y)=x2-5x+y2=(x-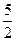 )2+y2-(
)2+y2-(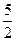 )2
)2
∴(x-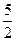 )2+y2=(
)2+y2=(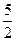 )2+
)2+
又|c|=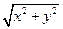 ∈[0, 5]
∈[0, 5]
∴向量c在以原点为圆心,5为半径的圆面上
即以(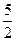 ,0)为圆心的圆,其半径最大值为
,0)为圆心的圆,其半径最大值为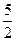
∴ 的最大值为0
的最大值为0
 =(c-a)?(c-b)=(1-x,-2-y)?(4-x,2-y)=x2-5x+y2=(x-
=(c-a)?(c-b)=(1-x,-2-y)?(4-x,2-y)=x2-5x+y2=(x-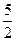 )2+y2-(
)2+y2-(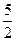 )2
)2∴(x-
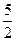 )2+y2=(
)2+y2=(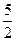 )2+
)2+
又|c|=
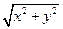 ∈[0, 5]
∈[0, 5]∴向量c在以原点为圆心,5为半径的圆面上
即以(
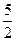 ,0)为圆心的圆,其半径最大值为
,0)为圆心的圆,其半径最大值为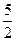
∴
 的最大值为0
的最大值为0
练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
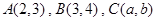 共线,则有( )
共线,则有( )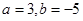
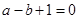
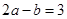
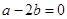
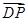 ,
,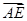 〉=
〉=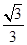 ,若以DA,DC,DP所在直线分别为x,y,z轴建立空间直角坐标系,则点E的坐标为________.
,若以DA,DC,DP所在直线分别为x,y,z轴建立空间直角坐标系,则点E的坐标为________.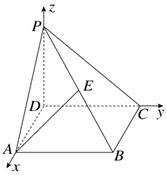
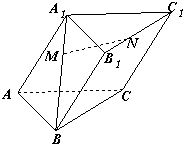
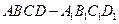 的棱长为2,则点
的棱长为2,则点 到平面
到平面 的距离是( )
的距离是( )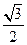
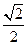
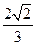
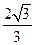
 ;
;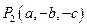 ;
; ;
;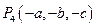 .
. 关于原点的对称点为
关于原点的对称点为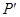 ,则
,则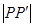 等于( )
等于( )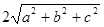
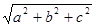
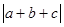

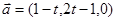 ,
,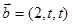 ,则
,则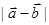 的最小值是
的最小值是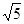
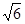
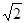
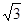
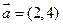 ,
,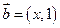 ,当
,当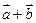 与
与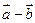 共线时,
共线时,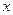 值为( )
值为( )