Question

【题目】如图，AB为圆柱的轴，CD为底面直径，E为底面圆周上一点，AB=1，CD=2，CE=DE．
求（1）三棱锥A﹣CDE的全面积；
（2）点D到平面ACE的距离．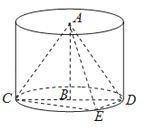

Answer 1

【答案】解：（1）∵AB为圆柱的轴，CD为底面直径，E为底面圆周上一点，AB=1，CD=2，CE=DE，
∴AD==，∠CED=90°，
∴DE=CE==AC=AD=AE，
∴三棱锥A﹣CDE的全面积：
S=S△CDE+S△ACD+S△ACE+S△ADE
=（X+2×1+XXsin600+XXsin600）
=2+．
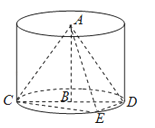
（2）设点D到平面ACE的距离为h，
由VA﹣CDE=VD﹣ACE ， 得，
∴h===．

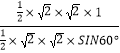【解析】（1）先求出AD= ， ∠CED=90°，DE=CE==AC=AD=AE，由此能求出三棱锥A﹣CDE的全面积．
（2）设点D到平面ACE的距离为h，由VA﹣CDE=VD﹣ACE ， 能求出点D到平面ACE的距离．