题目内容
已知函数,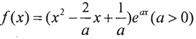 .
.
(1)求曲线f(x)在点A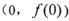 处的切线方程;
处的切线方程;
(II)讨论函数f(x)的单调性;
(III)是否存在实数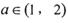 ,使
,使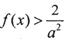 当
当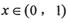 时恒成立?若存在,求 出实数a;若不存在,请说明理由
时恒成立?若存在,求 出实数a;若不存在,请说明理由
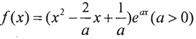 .
.(1)求曲线f(x)在点A
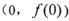 处的切线方程;
处的切线方程;(II)讨论函数f(x)的单调性;
(III)是否存在实数
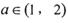 ,使
,使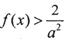 当
当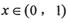 时恒成立?若存在,求 出实数a;若不存在,请说明理由
时恒成立?若存在,求 出实数a;若不存在,请说明理由(Ⅰ)∵ a>0, ,
,
∴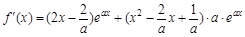
=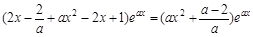 , …… 2分
, …… 2分
于是 ,
,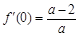 ,所以曲线y = f(x)在点A(0,f(0))处的切线方程为
,所以曲线y = f(x)在点A(0,f(0))处的切线方程为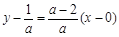 ,即(a-2)x-ay + 1 = 0. ……… 4分
,即(a-2)x-ay + 1 = 0. ……… 4分
(Ⅱ)∵ a>0,eax>0,∴ 只需讨论 的符号. ………… 5分
的符号. ………… 5分
ⅰ)当a>2时, >0,这时f ′(x)>0,所以函数f(x)在(-∞,+∞)上为增函数.
>0,这时f ′(x)>0,所以函数f(x)在(-∞,+∞)上为增函数.
ⅱ)当a = 2时,f ′(x)= 2x2e2x≥0,函数f(x)在(-∞,+∞)上为增函数.…6分
ⅲ)当0<a<2时,令f ′(x)= 0,解得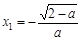 ,
,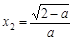 .
.
当x变化时, f '(x)和f(x)的变化情况如下表:
∴f(x)在 ,
,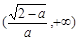 ,为增函数,f(x)在
,为增函数,f(x)在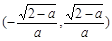 为减函数. …… 9分
为减函数. …… 9分
(Ⅲ)当a∈(1,2)时, ∈(0,1).由(Ⅱ)知f(x)在
∈(0,1).由(Ⅱ)知f(x)在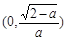 上是减函数,在
上是减函数,在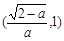 上是增函数,故当x∈(0,1)时,
上是增函数,故当x∈(0,1)时,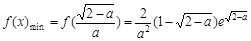 ,……10分
,……10分
∴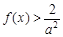 当x∈(0,1)时恒成立,等价于
当x∈(0,1)时恒成立,等价于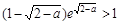 恒成立.……11分
恒成立.……11分
当a∈(1,2)时,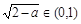 ,设
,设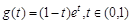 ,则
,则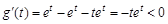 ,表明g(t) 在(0,1)上单调递减,于是可得
,表明g(t) 在(0,1)上单调递减,于是可得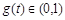 ,即a∈(1,2)时
,即a∈(1,2)时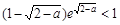 恒成立,……13分 符合条件的实数a不存在.
恒成立,……13分 符合条件的实数a不存在.
 ,
,∴
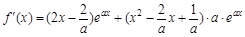
=
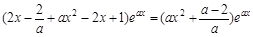 , …… 2分
, …… 2分于是
 ,
,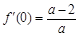 ,所以曲线y = f(x)在点A(0,f(0))处的切线方程为
,所以曲线y = f(x)在点A(0,f(0))处的切线方程为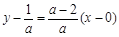 ,即(a-2)x-ay + 1 = 0. ……… 4分
,即(a-2)x-ay + 1 = 0. ……… 4分(Ⅱ)∵ a>0,eax>0,∴ 只需讨论
 的符号. ………… 5分
的符号. ………… 5分ⅰ)当a>2时,
 >0,这时f ′(x)>0,所以函数f(x)在(-∞,+∞)上为增函数.
>0,这时f ′(x)>0,所以函数f(x)在(-∞,+∞)上为增函数.ⅱ)当a = 2时,f ′(x)= 2x2e2x≥0,函数f(x)在(-∞,+∞)上为增函数.…6分
ⅲ)当0<a<2时,令f ′(x)= 0,解得
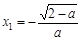 ,
,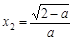 .
.当x变化时, f '(x)和f(x)的变化情况如下表:
| x |  | 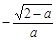 | 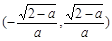 |  | 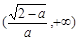 |
| f '(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
 ,
,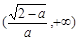 ,为增函数,f(x)在
,为增函数,f(x)在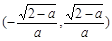 为减函数. …… 9分
为减函数. …… 9分(Ⅲ)当a∈(1,2)时,
 ∈(0,1).由(Ⅱ)知f(x)在
∈(0,1).由(Ⅱ)知f(x)在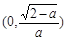 上是减函数,在
上是减函数,在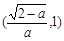 上是增函数,故当x∈(0,1)时,
上是增函数,故当x∈(0,1)时,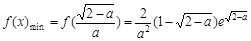 ,……10分
,……10分∴
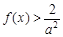 当x∈(0,1)时恒成立,等价于
当x∈(0,1)时恒成立,等价于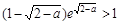 恒成立.……11分
恒成立.……11分 当a∈(1,2)时,
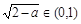 ,设
,设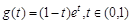 ,则
,则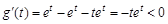 ,表明g(t) 在(0,1)上单调递减,于是可得
,表明g(t) 在(0,1)上单调递减,于是可得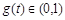 ,即a∈(1,2)时
,即a∈(1,2)时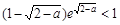 恒成立,……13分 符合条件的实数a不存在.
恒成立,……13分 符合条件的实数a不存在.略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
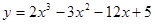 在
在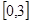 上的最大值为
上的最大值为 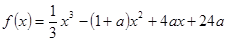 ,其中常数
,其中常数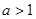
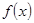 的单调性
的单调性 时,
时,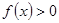 恒成立,求
恒成立,求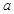 的取值范围
的取值范围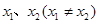 是函数
是函数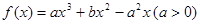 的两个极值点。
的两个极值点。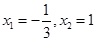 ,求函数
,求函数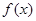 的解析式;
的解析式;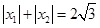 ,求
,求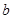 的最大值。
的最大值。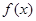 =3
=3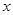 -4
-4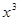 ,
,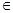 [0,1]的最大值是
[0,1]的最大值是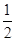

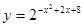
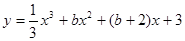 是R上的单调增函数,则
是R上的单调增函数,则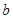 的取值范围是
的取值范围是 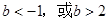
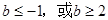
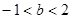
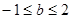
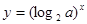 在R上为减函数,则
在R上为减函数,则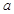 的取值范围 .
的取值范围 .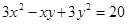 ,则
,则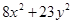 的最大值是 .
的最大值是 .