题目内容
【题目】已知函数![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值域;
的值域;
(2)当![]() 时,求
时,求![]() 的最小值
的最小值![]() ;
;
(3)是否存在实数![]() 、
、![]() ,同时满足下列条件:①
,同时满足下列条件:① ![]() ;② 当
;② 当![]() 的定义域为
的定义域为![]() 时,其值域为
时,其值域为![]() .若存在,求出
.若存在,求出![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1) ![]() (2)
(2)  (3) 不存在满足条件的实数
(3) 不存在满足条件的实数![]() 、
、![]() .见解析
.见解析
【解析】
(1)设t=3x,则φ(t)=t2﹣2at+3=(t﹣a)2+3﹣a2,φ(t)的对称轴为t=a,当a=1时,即可求出f(x)的值域;
(2)由函数φ(t)的对称轴为t=a,分类讨论当a![]() 时,当
时,当![]() a≤3时,当a>3时,求出最小值,则h(a)的表达式可求;
a≤3时,当a>3时,求出最小值,则h(a)的表达式可求;
(3)假设满足题意的m,n存在,函数h(a)在(3,+∞)上是减函数,求出h(a)的定义域,值域,然后列出不等式组,求解与已知矛盾,即可得到结论.
(1)当![]() 时,由
时,由![]() ,得
,得![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() .
.
(2)令![]() ,因为
,因为![]() ,故
,故![]() ,函数
,函数![]() 可化为
可化为
![]() .
.
① 当![]() 时,
时,![]() ;
;
② 当![]() 时,
时,![]() ;
;
③ 当![]() 时,
时,![]() .
.
综上,
(3)因为![]() ,
,![]() 为减函数,
为减函数,
所以![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
又![]() 在
在![]() 上的值域为
上的值域为![]() ,所以,
,所以,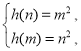 即
即
两式相减,得![]() ,
,
因为![]() ,所以
,所以![]() ,而由
,而由![]() 可得
可得![]() ,矛盾.
,矛盾.
所以,不存在满足条件的实数![]() 、
、![]() .
.

【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
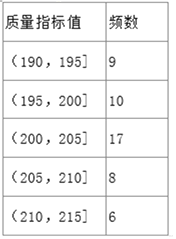
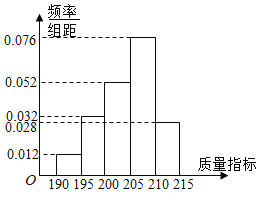
(1)根据频率分布直方图,估计乙流水线生产的产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲流水线 | 乙流水线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |