题目内容
5.设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x),当x∈[0,2]时,f(x)=2x-x2.(1)当x∈[2,4]时,求f(x)的解析式;
(2)计算:f(0)+f(1)+f(2)+…+f(201).
分析 (1)由题意可得f(x)=-f(x+2)=-(-f(x+4))=f(x+4);得到函数为周期函数;由[0,2]上的表达式先求[-2,0]上的表达式,再求[2,4]上的表达式;
(2)由周期性可化为f(0)+f(1)+f(2)+…+f(201)=50(f(0)+f(1)+f(2)+f(3))+f(0)=50(f(0)+f(1)+f(2)+f(-1))+f(0),再由奇偶性求解.
解答 解:(1)∵f(x+2)=-f(x),
∴f(x)=-f(x+2)=-(-f(x+4))=f(x+4);
故f(x)是以4为周期的周期函数;
∵当x∈[0,2]时,f(x)=2x-x2,
又∵f(x)是定义在R上的奇函数,
∴x∈[-2,0]时,f(x)=2x+x2,
故当x∈[2,4]时,f(x)=f(x-4)
=2(x-4)+(x-4)2
=x2-6x+8;
(2)∵f(x)是以4为周期的周期函数;
∴f(0)+f(1)+f(2)+…+f(201)
=50(f(0)+f(1)+f(2)+f(3))+f(0)
=50(f(0)+f(1)+f(2)+f(-1))+f(0)
=f(0)=0.
点评 本题考查了抽象函数的周期性与奇偶性的判断与应用,同时考查了函数解析式的求法,属于中档题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
15.A和B是抛物线y2=8x上除去原点以外的两个动点,O是坐标原点且满足$\overrightarrow{OA}•\overrightarrow{OB}$=0,$\overrightarrow{OM}•\overrightarrow{AB}$=0,则支动点M的轨迹方程为( )
| A. | x2+y2-8x=0 | B. | y=6x2 | C. | x2+4y2=1 | D. | $\frac{x^2}{9}-\frac{y^2}{4}$=1 |
20.已知数列{an},{bn}满足bn=log2an,n∈N*,其中{bn}是等差数列,且a8•a2008=$\frac{1}{4}$,则b1+b2+b3+…+b2015=( )
| A. | log22015 | B. | 2015 | C. | -2015 | D. | 1008 |
17.用秦九韶算法计算f(x)=x6-12x5+60x4-160x3+240x2-192x+64的值时,当x=2时,v4的值为( )
| A. | 0 | B. | 80 | C. | -80 | D. | -32 |
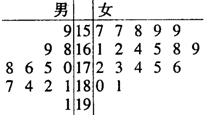 2013年8月28日-30日,第六届豫商大会在“三商之源、华商之都”的商丘市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如所示的茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.
2013年8月28日-30日,第六届豫商大会在“三商之源、华商之都”的商丘市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如所示的茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.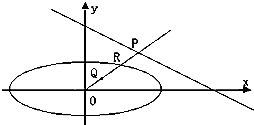 已知椭圆C:$\frac{{x}^{2}}{24}$+$\frac{{y}^{2}}{16}$=1,直线l:$\frac{x}{12}$+$\frac{y}{8}$=1.
已知椭圆C:$\frac{{x}^{2}}{24}$+$\frac{{y}^{2}}{16}$=1,直线l:$\frac{x}{12}$+$\frac{y}{8}$=1.