题目内容
【题目】已知动圆M经过点F(1,0),且与直线l:x=﹣1相切,动圆圆心M的轨迹记为曲线C
(1)求曲线C的轨迹方程
(2)若点P在y轴左侧(不含y轴)一点,曲线C上存在不同的两点A、B,满足PA,PB的中点都在曲线C上,设AB中点为E,证明:PE垂直于y轴.
【答案】(1)y2=4x(2)证明见解析
【解析】
(1)利用圆的半径相等列式化简方程即可.
(2)设A(![]() ,y1),B(
,y1),B(![]() ,y2),再求得中点,代入抛物线方程,再利用方程的根方法求解即可.
,y2),再求得中点,代入抛物线方程,再利用方程的根方法求解即可.
(1)设圆心M的坐标(x,y),由题意得:|MF|等于到直线l的距离,∴![]() |x+1|整理得:y2=4x,
|x+1|整理得:y2=4x,
所以曲线C的轨迹方程为:y2=4x;
(2)设P(x0,y0),由(1)设A(![]() ,y1),B(
,y1),B(![]() ,y2),
,y2),
AB的中点E(xE,yE),则yE![]() ,
,
因为PA的中点在抛物线上,
所以(![]() )2=4
)2=4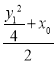 ,即:y12﹣2y0y1+8x0﹣y02=0;
,即:y12﹣2y0y1+8x0﹣y02=0;
同理可得PB的中点也在抛物线上可得:y22﹣2y0y2+8x0﹣y02=0,
所以y1,y2是方程:y2﹣2y0y+8x0﹣y02=0两个不同的根,
∴y1+y2=2y0,
所以yE=y0,
∴P与E的纵坐标相同,
所以PE垂直于y轴.

练习册系列答案
相关题目
【题目】为了分析某个高三学生的学习状态.现对他前5次考试的数学成绩x,物理成绩y进行分析.下面是该生前5次考试的成绩.
数学 | 120 | 118 | 116 | 122 | 124 |
物理 | 79 | 79 | 77 | 82 | 83 |
附 .
.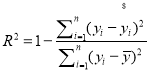 .
.
![]() 已知该生的物理成绩y与数学成绩x是线性相关的,求物理成绩y与数学成绩x的回归直线方程;
已知该生的物理成绩y与数学成绩x是线性相关的,求物理成绩y与数学成绩x的回归直线方程;
![]() 我们常用
我们常用![]() 来刻画回归的效果,其中
来刻画回归的效果,其中![]() 越接近于1,表示回归效果越好.求
越接近于1,表示回归效果越好.求![]() .
.
![]() 已知第6次考试该生的数学成绩达到132,请你估计第6次考试他的物理成绩大约是多少?
已知第6次考试该生的数学成绩达到132,请你估计第6次考试他的物理成绩大约是多少?
