题目内容
12.已知函数f(x)=x+$\frac{1}{{e}^{x}}$,若对任意x>0有f(x)>ax2-1恒成立,求a的取值范围.分析 利用分离常数法,求出a的不等式,构造函数g(x),求出g(x)的取值范围即得a的取值范围.
解答 解:当x∈(0,+∞)时,f(x)>ax2-1恒成立,
∴x+$\frac{1}{{e}^{x}}$>ax2-1,
即a<$\frac{1}{x}$+$\frac{1}{{x}^{2}{e}^{x}}$+$\frac{1}{{x}^{2}}$,
设g(x)=$\frac{1}{x}$+$\frac{1}{{x}^{2}{e}^{x}}$+$\frac{1}{{x}^{2}}$,其中x>0,
∴g′(x)=-$\frac{1}{{x}^{2}}$-$\frac{x+2}{{x}^{3}{e}^{x}}$-$\frac{2}{{x}^{3}}$<0在x>0恒成立,
g(x)在(0,+∞)上是单调减函数;
∴g(x)>0,即a≤0;
∴实数a的取值范围是(-∞,0].
点评 本题考查了函数的性质与应用问题,也考查了利用导数判断函数的单调性,不等式恒成立问题注意转化为求函数的最值问题,是综合性题目.

练习册系列答案
相关题目
2.在3x+2y<6表示的平面区域内的一个点是( )
| A. | (3,0) | B. | (1,3) | C. | (0,3) | D. | (0,0) |
3.设全集U=R,A={x||x|<2},B={x|y=$\sqrt{x-1}$},则图中阴影部分所表示的集合( )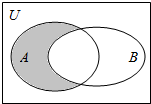

| A. | (-2,+∞) | B. | (1,2] | C. | (-2,1) | D. | (-2,1] |
20.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(∁UA)∩B=( )
| A. | {2} | B. | {2,4} | C. | {0,4} | D. | {4} |
2.椭圆C:$\frac{x^2}{16}+\frac{y^2}{9}$=1的左、右顶点分别为A1,A2,点P是C上异于顶点的任一点,则直线PA2与直线PA1的斜率之积是( )
| A. | -$\frac{3}{4}$ | B. | -$\frac{9}{16}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{16}{9}$ |