题目内容
【题目】在平面直角坐标系![]() 中,已知双曲线
中,已知双曲线![]() .
.
(1)过曲线![]() 的左顶点作
的左顶点作![]() 的两条渐近线的平行线,求这两组平行线围成的平行四边形的面积;
的两条渐近线的平行线,求这两组平行线围成的平行四边形的面积;
(2)设斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,若
两点,若![]() 与圆
与圆![]() 相切,求证:
相切,求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)求出双曲线![]() 的左顶点
的左顶点![]() 的坐标和渐近线方程,求出过曲线
的坐标和渐近线方程,求出过曲线![]() 的左顶点作
的左顶点作![]() 的渐近线的平行线方程,求出直线
的渐近线的平行线方程,求出直线![]() 与直线
与直线![]() 的交点坐标,进而可求得由这两组平行线围成的平行四边形的面积;
的交点坐标,进而可求得由这两组平行线围成的平行四边形的面积;
(2)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,由直线
,由直线![]() 与圆相切得出
与圆相切得出![]() ,再将直线
,再将直线![]() 的方程与双曲线
的方程与双曲线![]() 的方程联立,列出韦达定理,利用平面向量数量积的坐标运算和韦达定理,计算出
的方程联立,列出韦达定理,利用平面向量数量积的坐标运算和韦达定理,计算出![]() ,由此能证明出
,由此能证明出![]() .
.
(1)左顶点 ,渐近线方程为
,渐近线方程为![]() ,
,
过点![]() 与渐近线
与渐近线![]() 平行的直线方程为
平行的直线方程为 ,即
,即![]() .
.
解方程组 ,得
,得 ,
,
因此,所求平行四边形的面积![]() ;
;
(2)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,
,
因直线![]() 与圆
与圆![]() 相切,故
相切,故![]() ,即
,即![]() .
.
由![]() ,得
,得![]() .
.
由韦达定理得![]() ,
,![]() ,
,
![]()
![]() ,
,
因此,![]() .
.

 步步高达标卷系列答案
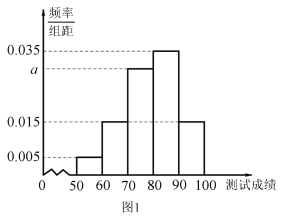
步步高达标卷系列答案【题目】顺义区教委对本区高一,高二年级学生体质健康测试成绩进行抽样分析.学生测试成绩满分为100分,90分及以上为优秀,60分以下为不及格.先从两个年级各抽取100名学生的测试成绩.其中高一年级学生测试成绩统计结果如图1,高二年级学生测试成绩统计结果如表1.
分组 | 人数 |
|
|
|
|
|
|
|
|
|
|
表1
(1)求图1中a的值;
(2)为了调查测试成绩不及格的同学的具体情况,决定从样本中不及格的学生中抽取3人,用X表示抽取的3人中高二年级的学生人数.求X的分布列及均值;
(3)若用以上抽样数据估计全区学生体质健康情况.用Y表示从全区高二年级全部学生中任取3人中成绩优秀的人数,求EY的值;
(4)用![]() ,
,![]() ,分别表示样本中高一,高二年级学生测试成绩的方差,比较其大小(只需写出结果).
,分别表示样本中高一,高二年级学生测试成绩的方差,比较其大小(只需写出结果).
【题目】王明、李东、张红三位同学在第一、第二学期消费的部分文具的数量如表所示:
姓名 | 第一学期 | 第二学期 | ||||||
笔记本 | 练习本 | 水笔 | 铅笔 | 笔记本 | 练习本 | 水笔 | 铅笔 | |
王明 | 3 | 5 | 2 | 4 | 4 | 6 | 3 | 3 |
李东 | 2 | 6 | 3 | 3 | 4 | 8 | 5 | 2 |
张红 | 4 | 7 | 4 | 2 | 5 | 10 | 6 | 4 |
若笔记本的单价为每本5元;练习本每本2元;水笔每支3元;铅笔每支1元.求三位学生在这些文具上各自花费的金额.