题目内容
7．设a=log50.4，b=2-0.2，c=log45，则a，b，c的大小关系是a＜b＜c．分析 根据指数函数、对数函数的图象与性质，利用特殊值，即可比较a，b，c的大小．
解答 解：∵a=log50.4＜log51=0，
b=2-0.2＞0，且b=2-0.2＜20=1，
c=log45＞log44=1；
∴a＜0＜b＜1＜c，
即a，b，c的大小关系是a＜b＜c．
故答案为：a＜b＜c．
点评 本题考查了指数函数和对数函数的图象与性质的应用问题，是基础题目．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
17．函数y=$\sqrt{\frac{1}{4}-si{n}^{2}x}$+|sinx|的值域是（ ）
| A． | [-$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{2}}{2}$] | B． | [0，$\frac{\sqrt{2}}{2}$] | C． | [0，$\frac{\sqrt{3}}{2}$] | D． | [$\frac{1}{2}$，$\frac{\sqrt{2}}{2}$] |
18．在直角坐标系平面中，已知点P1（1，2），P2（2，22），P3（3，23），…，Pn（n，2n），其中n是正整数，对于平面上任意一点A0，记A1为A0关于点P1的对称点，A2为A1关于点P2的对称点，…，An为An-1关于点Pn的对称点，则对任意偶数n，用n表示向量$\overrightarrow{{A}_{0}{A}_{n}}$的坐标为（ ）
| A． | （n，$\frac{4（{2}^{n}-1）}{3}$） | B． | （n，$\frac{{2}^{n+2}}{3}$） | C． | （$\frac{n}{2}$，$\frac{2（{2}^{n}-1）}{3}$） | D． | （$\frac{n}{2}$，$\frac{{2}^{n+1}}{3}$） |
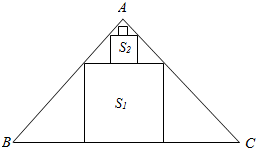在等腰直角△ABC中，∠A=90°，BC=6，△ABC中排列着内接正方形，如图所示，若正方形的面积依次为S1，S2，…，Sn，…（从大到小），其中n∈N+，则$\underset{lim}{n→∞}$（S1+S2+…+Sn）=$\frac{9}{2}$．
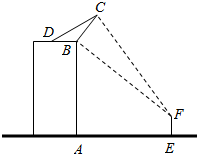如图，一楼房高AB为19$\sqrt{3}$米，某广告公司在楼顶安装一块宽BC为4米的广告牌，CD为拉杆，广告牌的倾角为60°，安装过程中，一身高为$\sqrt{3}$米的监理人员EF站在楼前观察该广传牌的安装效果：为保证安全，该监理人员不得站在广告牌的正下方：设AE=x米，该监理人员观察广告牌的视角∠BFC=θ．