题目内容
【题目】已知函数f(x)= 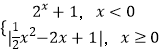 ,方程f2(x)﹣af(x)+b=0(b≠0)有六个不同的实数解,则3a+b的取值范围是( )
,方程f2(x)﹣af(x)+b=0(b≠0)有六个不同的实数解,则3a+b的取值范围是( )
A.[6,11]
B.[3,11]
C.(6,11)
D.(3,11)
【答案】D
【解析】解:作函数f(x)=  的图象如下,
的图象如下,
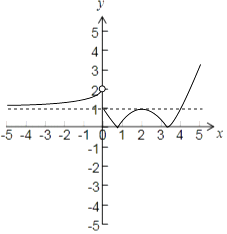
∵关于x的方程f2(x)﹣af(x)+b=0有6个不同实数解,
令t=f(x),
∴t2﹣at+b=0有2个不同的正实数解,
其中一个为在(0,1)上,一个在(1,2)上;
故  ,
,
其对应的平面区域如下图所示:

故当a=3,b=2时,3a+b取最大值11,
当a=1,b=0时,3a+b取最小值3,
则3a+b的取值范围是(3,11)
故选:D
作函数f(x)=  的图象,从而利用数形结合知t2﹣at+b=0有2个不同的正实数解,且其中一个为1,从而可得﹣1﹣a>0且﹣1﹣a≠1;从而解得.
的图象,从而利用数形结合知t2﹣at+b=0有2个不同的正实数解,且其中一个为1,从而可得﹣1﹣a>0且﹣1﹣a≠1;从而解得.

练习册系列答案
相关题目
【题目】为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换.已知某校使用的100只日光灯在必须换掉前的使用天数如下表:
天数/天 | 151~180 | 181~210 | 211~240 | 241~270 | 271~300 | 301~330 | 331~360 | 361~390 |
灯管数/只 | 1 | 11 | 18 | 20 | 25 | 16 | 7 | 2 |
(1)试估计这种日光灯的平均使用寿命;
(2)若定期更换,可选择多长时间统一更换合适?