题目内容
某售报亭每天以每份0.4元的价格从报社购进若干份报纸,然后以每份1元的价格出售,如果当天卖不完,剩下的报纸以每份0.1元的价格卖给废品收购站.
(Ⅰ)若售报亭一天购进270份报纸,求当天的利润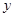 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:份,
(单位:份,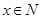 )的函数解析式.
)的函数解析式.
(Ⅱ)售报亭记录了100天报纸的日需求量(单位:份),整理得下表:
日需求量 | 240 | 250 | 260 | 270 | 280 | 290 | 300 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
(1)若售报亭一天购进270份报纸,
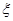 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求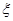 的数学期望;
的数学期望;(2)若售报亭计划每天应购进270份或280份报纸,你认为购进270份报纸好,还是购进280份报纸好? 说明理由.
(Ⅰ)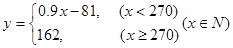 (Ⅱ)(1)
(Ⅱ)(1)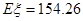 (2)每天购进280张报纸好,此时利润最高.
(2)每天购进280张报纸好,此时利润最高.
解析试题分析:(Ⅰ)当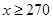 时,
时,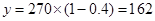 ;
;
当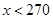 时,
时, ,
,
∴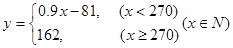 ……5分
……5分
(Ⅱ)(1)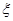 可取135、144、153、162, 则
可取135、144、153、162, 则 ,
,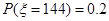 ,
,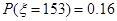 ,
,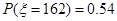 .
.
∴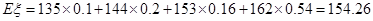 . ……9分
. ……9分
(2)购进报纸280张,当天的利润为
 ,
,
所以每天购进280张报纸好 ……12分
考点:本小题主要考查用函数解决实际问题,离散型随机变量的期望和最优化问题.
点评:解决实际问题,关键是根据题意进行准确转化,转化为熟悉的数学模型解决问题.

练习册系列答案
相关题目
 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.
 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域; ;写出图2表示的种植成本与时间的函数关系式
;写出图2表示的种植成本与时间的函数关系式 .
.
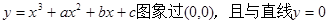 在原点相切,若函数的极小值为
在原点相切,若函数的极小值为 ;
;
 的定义域为
的定义域为 ,对任意的实数
,对任意的实数 都有
都有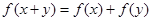 ;当
;当 时,
时, ,且
,且 .(1)判断并证明
.(1)判断并证明 上的单调性;
上的单调性; 满足:
满足: ,且
,且 ,证明:对任意的
,证明:对任意的 ,
,
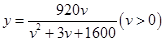 .
.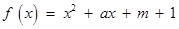 ,关于
,关于 的不等式
的不等式 的解集为
的解集为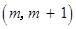 ,其中
,其中 为非零常数.设
为非零常数.设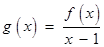 .
. 的值;
的值;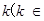 R
R 如何取值时,函数
如何取值时,函数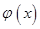
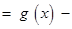
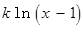 存在极值点,并求出极值点;
存在极值点,并求出极值点;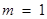 ,且
,且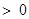 ,求证:
,求证: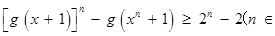 N
N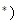
 套世博吉祥物“海宝”所需成本费用为
套世博吉祥物“海宝”所需成本费用为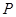 元,且
元,且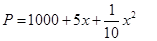 ,而每套“海宝”售出的价格为
,而每套“海宝”售出的价格为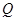 元,其中
元,其中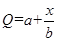
 ,
,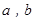 的值.(利润 = 销售收入-成本)
的值.(利润 = 销售收入-成本)