题目内容
设某市现有从事第二产业人员100万人,平均每人每年创造产值a万元(a为正常数),现在决定从中分流x万人去加强第三产业。分流后,继续从事第二产业的人员平均每人每年创造产值可增加2x%(0<x<100)。而分流出的从事第三产业的人员,平均每人每年可创造产值1.2a万元。
(1)若要保证第二产业的产值不减少,求x的取值范围;
(2)在(1)的条件下,问应分流出多少人,才能使该市第二、三产业的总产值增加最多?
(1)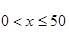 (2)应分流出50万人才能使该市第二、三产业的总产值增加最多
(2)应分流出50万人才能使该市第二、三产业的总产值增加最多
解析试题分析:(1)由题意,得 4分
4分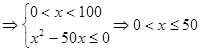 7分
7分
(2)设该市第二、三产业的总产值增加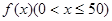 万元,则
万元,则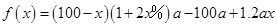
=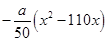 =
=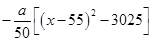 10分
10分
∵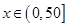 时,
时, 单调递增,∴
单调递增,∴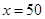 时,
时,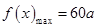 14分
14分
即应分流出50万人才能使该市第二、三产业的总产值增加最多 16分
考点:本题考查了函数的实际运用
点评:在解决某些应用问题时,通常要用到一些函数模型,它们主要是:一次函数模型、
二次函数模型、指数函数模型、对数函数模型、幂函数模型、分式函数模型、分段函数模型等。

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
某售报亭每天以每份0.4元的价格从报社购进若干份报纸,然后以每份1元的价格出售,如果当天卖不完,剩下的报纸以每份0.1元的价格卖给废品收购站.
(Ⅰ)若售报亭一天购进270份报纸,求当天的利润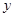 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:份,
(单位:份,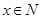 )的函数解析式.
)的函数解析式.
(Ⅱ)售报亭记录了100天报纸的日需求量(单位:份),整理得下表:
日需求量 | 240 | 250 | 260 | 270 | 280 | 290 | 300 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
(1)若售报亭一天购进270份报纸,
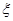 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求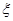 的数学期望;
的数学期望;(2)若售报亭计划每天应购进270份或280份报纸,你认为购进270份报纸好,还是购进280份报纸好? 说明理由.
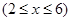 .
.
 .
.  ;
;  ,求证:
,求证: ≤
≤ .
. (元)与月处理量
(元)与月处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.  与科技成本的投入次数
与科技成本的投入次数 的关系是
的关系是 .若水晶产品的销售价格不变,第
.若水晶产品的销售价格不变,第 万元.
万元.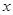 万件,需另投入流动成本为
万件,需另投入流动成本为 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,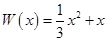 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,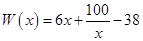 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完. (万元)关于年产量
(万元)关于年产量 固定成本
固定成本
