题目内容
(本题满分15分)
经过长期的观测得到:在交通繁忙时段,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为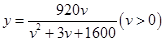 .
.
(1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?
(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
(1)当汽车的平均速度v为40千米/小时时,车流量最大,最大车流量为11.1千辆/小时.
(2)当汽车的平均速度大于25千米/小时,小于64千米/小时时,该时段内车流量超过10千辆/小时.
解析试题分析:(1)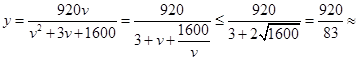 11.1,
11.1,
当且仅当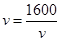 ,即
,即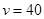 时,上式取等号.
时,上式取等号.
所以,当汽车的平均速度v为40千米/小时时,车流量最大,最大车流量为11.1千辆/小时.
(2)由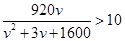 得,
得,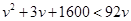 ,即
,即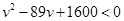 ,
,
解得 25<v<64.
所以,当汽车的平均速度大于25千米/小时,小于64千米/小时时,该时段内车流量超过10千辆/小时.
考点:本题主要考查函数模型,利用导数研究函数单调性、求函数极值、最值,均值定理的应用。
点评:典型题,导数的应用,是高考必考内容,注意解答成立问题的一般方法步骤。构建函数模型是关键,在求函数最值的过程中,可以运用“导数法”,也可根据题目特点,选用“均值定理”。应用均值定理时,要注意“一正、二定、三相等”缺一不可。

 阅读快车系列答案
阅读快车系列答案某售报亭每天以每份0.4元的价格从报社购进若干份报纸,然后以每份1元的价格出售,如果当天卖不完,剩下的报纸以每份0.1元的价格卖给废品收购站.
(Ⅰ)若售报亭一天购进270份报纸,求当天的利润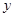 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:份,
(单位:份,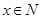 )的函数解析式.
)的函数解析式.
(Ⅱ)售报亭记录了100天报纸的日需求量(单位:份),整理得下表:
日需求量 | 240 | 250 | 260 | 270 | 280 | 290 | 300 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
(1)若售报亭一天购进270份报纸,
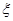 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求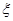 的数学期望;
的数学期望;(2)若售报亭计划每天应购进270份或280份报纸,你认为购进270份报纸好,还是购进280份报纸好? 说明理由.



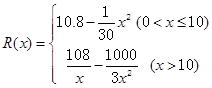
 ,若
,若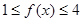 对一切
对一切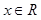 恒成立.求实数
恒成立.求实数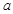 的取值范围.(16分)
的取值范围.(16分)  (2)
(2)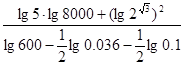
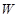 与它的航行速度
与它的航行速度 (公里/小时)的函数关系式;
(公里/小时)的函数关系式;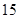 元,销售价是
元,销售价是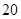 元,月平均销售
元,月平均销售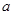 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为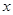
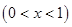 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为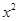 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是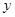 (元).
(元).