题目内容
设函数 的定义域为
的定义域为 ,对任意的实数
,对任意的实数 都有
都有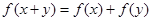 ;当
;当 时,
时, ,且
,且 .(1)判断并证明
.(1)判断并证明 在
在 上的单调性;
上的单调性;
(2)若数列 满足:
满足: ,且
,且 ,证明:对任意的
,证明:对任意的 ,
,
(1)单调递增(2)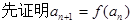 ,再利用
,再利用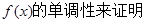 .
.
解析试题分析:(1) 在
在 上单调递增,证明如下: 设任意
上单调递增,证明如下: 设任意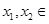
 ,且
,且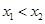 ,∵
,∵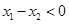 ,∴
,∴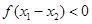 ,∴
,∴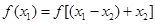
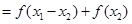
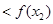
即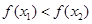 ,∴
,∴ 在
在 上单调递增.
上单调递增.
(2)在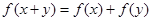 中,令
中,令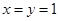 ,得
,得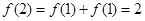 .令
.令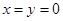 ,
,
得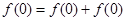 ,∴
,∴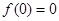 .令
.令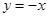 ,得
,得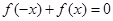 ,即
,即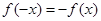

下面用数学归纳法证明:
①当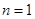 时,
时, ,不等式成立;
,不等式成立;
②假设当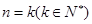 时,不等式成立,即
时,不等式成立,即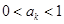 ,则∵
,则∵ 在
在 上单调递增,
上单调递增,
∴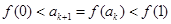 ,∴
,∴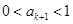 ,即当
,即当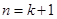 时不等式也成立.
时不等式也成立.
综上①②,由数学归纳法原理可知对任意的 ,
,
考点:数学归纳法;抽象函数及其应用;数列与函数的综合
点评:本题考查函数的单调性,考查数学归纳法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
某售报亭每天以每份0.4元的价格从报社购进若干份报纸,然后以每份1元的价格出售,如果当天卖不完,剩下的报纸以每份0.1元的价格卖给废品收购站.
(Ⅰ)若售报亭一天购进270份报纸,求当天的利润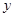 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:份,
(单位:份,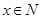 )的函数解析式.
)的函数解析式.
(Ⅱ)售报亭记录了100天报纸的日需求量(单位:份),整理得下表:
日需求量 | 240 | 250 | 260 | 270 | 280 | 290 | 300 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
(1)若售报亭一天购进270份报纸,
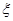 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求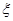 的数学期望;
的数学期望;(2)若售报亭计划每天应购进270份或280份报纸,你认为购进270份报纸好,还是购进280份报纸好? 说明理由.
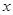 万件,需另投入流动成本为
万件,需另投入流动成本为 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,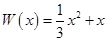 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,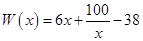 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.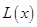 (万元)关于年产量
(万元)关于年产量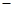 固定成本
固定成本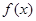 有两个零点
有两个零点 和
和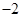 ,且
,且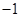 ,函数
,函数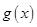 与
与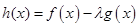 在区间
在区间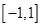 上是增函数,求实数
上是增函数,求实数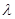 的取值范围。
的取值范围。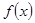 是定义在实数集R上的函数,满足
是定义在实数集R上的函数,满足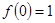 ,且对任意实数a,b有
,且对任意实数a,b有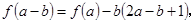 求
求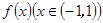 满足
满足 求
求 且关于
且关于 的方程
的方程 在
在 上有两个不相等的实数根.⑴求
上有两个不相等的实数根.⑴求 的解析式.⑵若
的解析式.⑵若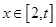 总有
总有 成立,求
成立,求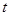 的最大值.
的最大值. ,若
,若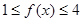 对一切
对一切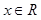 恒成立.求实数
恒成立.求实数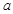 的取值范围.(16分)
的取值范围.(16分) 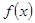 的定义域是
的定义域是 ,且满足
,且满足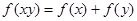 ,
,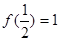 ,如果对于0<x<y,都有
,如果对于0<x<y,都有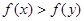 ,
,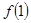 ;
;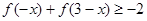
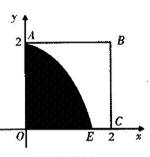
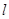 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数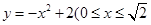 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为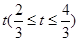 .
.
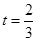 时,求直路
时,求直路