题目内容
已知函数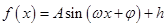
 的图象如图所示.
的图象如图所示.
(1)求函数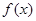 的解析式;
的解析式;
(2)设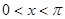 ,且方程
,且方程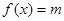 有两个不同的实数根,求实数
有两个不同的实数根,求实数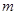 的取值范围和这两个根的和;
的取值范围和这两个根的和;
(3)在锐角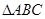 中,若
中,若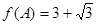 ,求
,求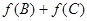 的取值范围.
的取值范围.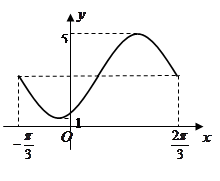
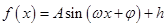
 的图象如图所示.
的图象如图所示.(1)求函数
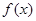 的解析式;
的解析式;(2)设
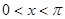 ,且方程
,且方程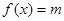 有两个不同的实数根,求实数
有两个不同的实数根,求实数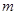 的取值范围和这两个根的和;
的取值范围和这两个根的和;(3)在锐角
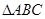 中,若
中,若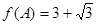 ,求
,求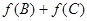 的取值范围.
的取值范围.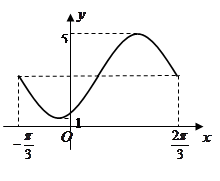
见解析
(1)依据A,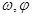 的意义,结合条件便可求得;(2)利用数形结合思想求出m的取值范围,利用对称性求出方程根的和;(3)利用二倍角和诱导公式化简函数,然后利用三角函数的有界性求得函数的值域。
的意义,结合条件便可求得;(2)利用数形结合思想求出m的取值范围,利用对称性求出方程根的和;(3)利用二倍角和诱导公式化简函数,然后利用三角函数的有界性求得函数的值域。
由图易知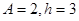 又
又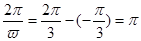 ∴
∴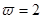
又由图知当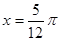 时,
时,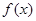 取最大值5,
取最大值5,
∴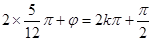 ,即
,即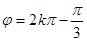 ,
,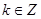
又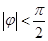 ∴
∴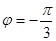 故:
故: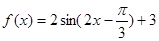 ……2分
……2分
(2)∵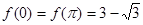 由图象知,
由图象知,
要使方程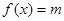 有两个不同的实数根,有
有两个不同的实数根,有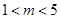 且
且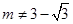 …3分
…3分
当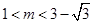 时, 方程的两根关于直线
时, 方程的两根关于直线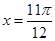 对称,则两根之和为
对称,则两根之和为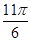
当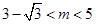 时, 方程的两根关于直线
时, 方程的两根关于直线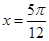 对称,则两根之和为
对称,则两根之和为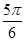 ……4分
……4分
(3)∵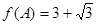 , ∴
, ∴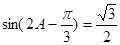 ∴
∴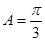 (∵
(∵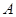 为锐角)……5分
为锐角)……5分
∴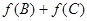 =
=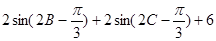
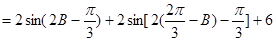
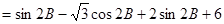
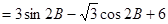
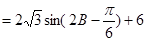 …7分
…7分
又由锐角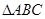 及
及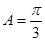 ,得
,得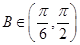 ,∴
,∴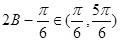
∴ ∴
∴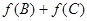
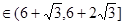
 的意义,结合条件便可求得;(2)利用数形结合思想求出m的取值范围,利用对称性求出方程根的和;(3)利用二倍角和诱导公式化简函数,然后利用三角函数的有界性求得函数的值域。
的意义,结合条件便可求得;(2)利用数形结合思想求出m的取值范围,利用对称性求出方程根的和;(3)利用二倍角和诱导公式化简函数,然后利用三角函数的有界性求得函数的值域。由图易知
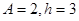 又
又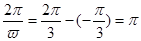 ∴
∴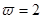
又由图知当
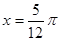 时,
时,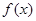 取最大值5,
取最大值5,∴
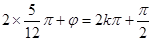 ,即
,即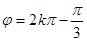 ,
,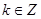
又
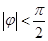 ∴
∴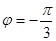 故:
故: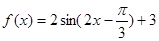 ……2分
……2分(2)∵
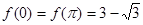 由图象知,
由图象知,要使方程
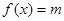 有两个不同的实数根,有
有两个不同的实数根,有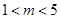 且
且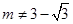 …3分
…3分当
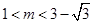 时, 方程的两根关于直线
时, 方程的两根关于直线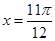 对称,则两根之和为
对称,则两根之和为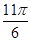
当
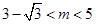 时, 方程的两根关于直线
时, 方程的两根关于直线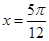 对称,则两根之和为
对称,则两根之和为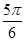 ……4分
……4分(3)∵
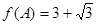 , ∴
, ∴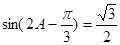 ∴
∴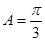 (∵
(∵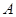 为锐角)……5分
为锐角)……5分∴
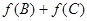 =
=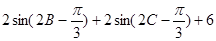
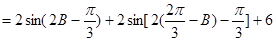
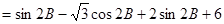
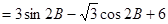
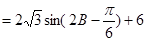 …7分
…7分又由锐角
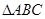 及
及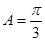 ,得
,得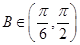 ,∴
,∴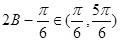
∴
 ∴
∴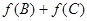

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 的图象与
的图象与 轴交点的纵坐标为1,在相邻的两点
轴交点的纵坐标为1,在相邻的两点 ,
, 上
上 分别取得最大值和最小值.
分别取得最大值和最小值. 的最大和最小值分别为6和2,求
的最大和最小值分别为6和2,求 的值.
的值.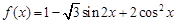 .
.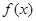 的最大值及取得最大值时的
的最大值及取得最大值时的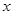 集合;
集合;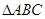 的角
的角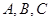 的对边分别为
的对边分别为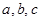 ,且
,且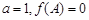 .求
.求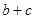 的取值范围
的取值范围 在
在 上有两个不等的实数根
上有两个不等的实数根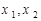 ,则
,则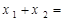 ( )
( )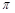
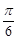
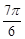
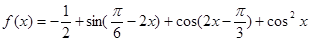
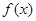 的最小正周期;
的最小正周期;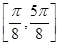 上的最大值,并求出
上的最大值,并求出 满足:
满足: ,点
,点 满足:
满足: 则
则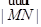 的最小值是
的最小值是



 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为
 时,求f(x)的值域.
时,求f(x)的值域.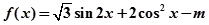 。
。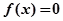 在
在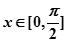 上有解,求
上有解,求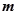 的取值范围;
的取值范围;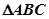 中,
中,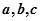 分别是
分别是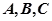 所对的边,当(1)中的
所对的边,当(1)中的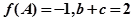 时,求
时,求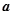 的最小值。
的最小值。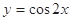 的图象,可由函数
的图象,可由函数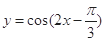 的图像( )
的图像( )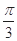 个长度单位
个长度单位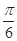 个长度单位
个长度单位