题目内容
(本小题满分12分)已知函数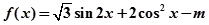 。
。
(1)若方程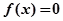 在
在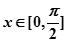 上有解,求
上有解,求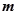 的取值范围;
的取值范围;
(2)在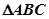 中,
中,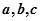 分别是
分别是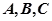 所对的边,当(1)中的
所对的边,当(1)中的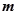 取最大值,且
取最大值,且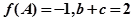 时,求
时,求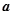 的最小值。
的最小值。
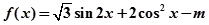 。
。(1)若方程
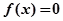 在
在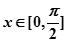 上有解,求
上有解,求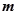 的取值范围;
的取值范围;(2)在
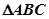 中,
中,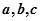 分别是
分别是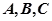 所对的边,当(1)中的
所对的边,当(1)中的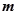 取最大值,且
取最大值,且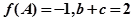 时,求
时,求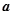 的最小值。
的最小值。(1)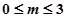 ;(2)a有最小值1,此时
;(2)a有最小值1,此时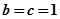
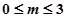 ;(2)a有最小值1,此时
;(2)a有最小值1,此时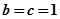
第一问利用方程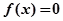 在
在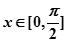 上有解
上有解
即
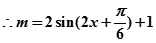 在
在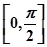 内有解
内有解
结合三角函数性质可得。
第二问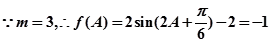 ,
,
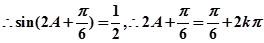 或
或
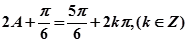
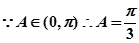
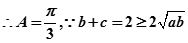 ,当且仅当
,当且仅当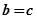 时
时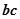 有最大值1
有最大值1
解:(1) ,
,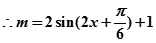 在
在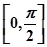 内有解…3
内有解…3
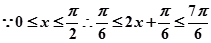
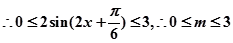 …5
…5
(2)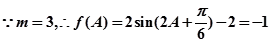 ,
,
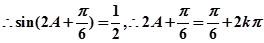 或
或
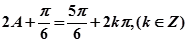
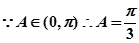 ……7
……7
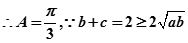 ,当且仅当
,当且仅当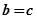 时
时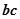 有最大值1。 ……9
有最大值1。 ……9
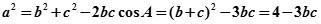 ,…10
,…10
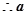 有最小值1,此时
有最小值1,此时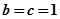 …12
…12
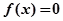 在
在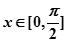 上有解
上有解即

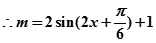 在
在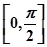 内有解
内有解结合三角函数性质可得。
第二问
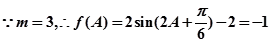 ,
, 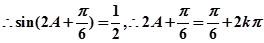 或
或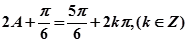
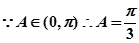
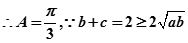 ,当且仅当
,当且仅当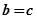 时
时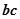 有最大值1
有最大值1解:(1)
 ,
,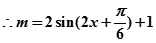 在
在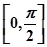 内有解…3
内有解…3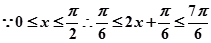
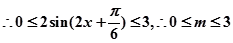 …5
…5(2)
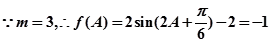 ,
, 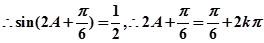 或
或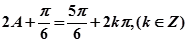
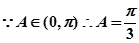 ……7
……7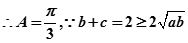 ,当且仅当
,当且仅当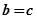 时
时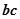 有最大值1。 ……9
有最大值1。 ……9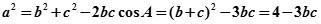 ,…10
,…10 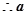 有最小值1,此时
有最小值1,此时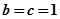 …12
…12
练习册系列答案
相关题目
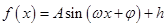
 的图象如图所示.
的图象如图所示.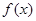 的解析式;
的解析式;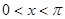 ,且方程
,且方程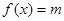 有两个不同的实数根,求实数
有两个不同的实数根,求实数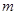 的取值范围和这两个根的和;
的取值范围和这两个根的和;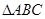 中,若
中,若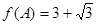 ,求
,求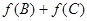 的取值范围.
的取值范围.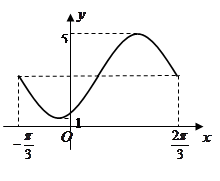
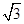 cosωx+sinωx)+
cosωx+sinωx)+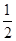 (ω∈R,x∈R)最小正周期为π,且图象关于直线x=
(ω∈R,x∈R)最小正周期为π,且图象关于直线x=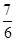 π对称.
π对称.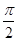 ]的图象有且只有一个公共点,求实数a的范围.
]的图象有且只有一个公共点,求实数a的范围.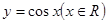 的图像向左平移
的图像向左平移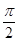 个单位后,得到
个单位后,得到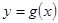 的图像,
的图像,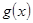 的解析式为( )
的解析式为( )
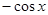
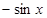

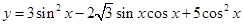 的值域为 ▲ .
的值域为 ▲ . 的三个内角为
的三个内角为 、
、 、
、 ,当
,当 取得最大值,且这个最大值为
取得最大值,且这个最大值为 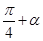 )=
)=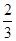 ,则
,则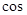 (
(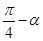 )的值等于( )
)的值等于( )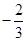
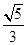
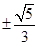
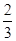 ,则sinA+cosA=( )
,则sinA+cosA=( )

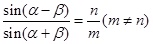 ,则
,则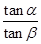 = ( )
= ( )