题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值;
上的最小值;
(2)若![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)由![]() 得
得![]() ,对其求导,解对应的不等式,判断单调性,即可得出最值;
,对其求导,解对应的不等式,判断单调性,即可得出最值;
(2)先对函数求导,得到![]() ,根据
,根据![]() ,判断函数
,判断函数![]() 的单调性,求出最小值,再由导数的方法研究
的单调性,求出最小值,再由导数的方法研究![]() 最小值的范围,即可证明结论成立.
最小值的范围,即可证明结论成立.
(1)当![]() 时,由
时,由![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() .
.
(2)由题意,函数的定义域为![]() ,
,![]() ,
,
令![]() ,
,![]() ,则
,则![]() ,设
,设![]() ,则
,则![]() ,
,
易知![]() 在
在![]() 上单调递增,
上单调递增,
∵![]() ,∴
,∴![]() ,
,![]() ,所以存在唯一的
,所以存在唯一的![]() ,使
,使![]() ,
,
当![]() 时,
时,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
又∵![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上无零点,
上无零点,
∴存在唯一的![]() ,使
,使![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 单调递增.
单调递增.
∴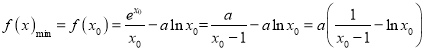 ,
,![]() .
.
令![]() ,则
,则![]() 在
在![]() 上单调递减,
上单调递减,
∵![]() ∴
∴![]() ,又∵
,又∵![]() ∴
∴![]() ,从而
,从而![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
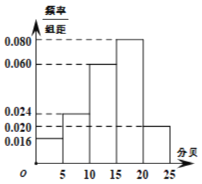
【题目】在中老年人群体中,肠胃病是一种高发性疾病某医学小组为了解肠胃病与运动之间的联系,调查了50位中老年人每周运动的总时长(单位:小时),将数据分成[0,4),[4,8),[8,14),[14,16),[16,20),[20,24]6组进行统计,并绘制出如图所示的柱形图.
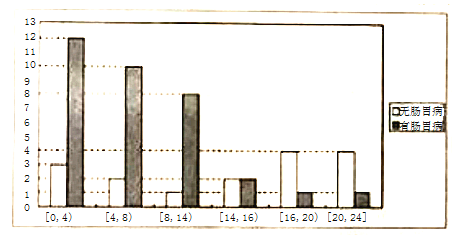
图中纵轴的数字表示对应区间的人数现规定:每周运动的总时长少于14小时为运动较少.
每周运动的总时长不少于14小时为运动较多.
(1)根据题意,完成下面的2×2列联表:
有肠胃病 | 无肠胃病 | 总计 | |
运动较多 | |||
运动较少 | |||
总计 |
(2)能否有99.9%的把握认为中老年人是否有肠胃病与运动有关?
附:K2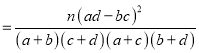 (n=a+b+c+d)
(n=a+b+c+d)
P(K2≥k) | 0.0.50 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |