题目内容
【题目】已知函数![]() ,其中
,其中![]() ,e是自然对数的底数.
,e是自然对数的底数.
(1)若![]() 是
是![]() 上的增函数,求实数a的取值范围;
上的增函数,求实数a的取值范围;
(2)若![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)由![]() 是
是![]() 上的增函数等价于
上的增函数等价于![]() 恒成立,得
恒成立,得![]() ,求
,求![]() 的最大值,即可得到本题答案;
的最大值,即可得到本题答案;
(2)由![]() ,证明当
,证明当![]() 时,
时,![]() 的最小值大于0,即可得到本题答案.
的最小值大于0,即可得到本题答案.
解:(1)![]() ,
,![]() 是
是![]() 上的增函数等价于
上的增函数等价于![]() 恒成立.
恒成立.
令![]() ,得
,得![]() ,令
,令![]() .以下只需求
.以下只需求![]() 的最大值.
的最大值.
求导得![]() ,令
,令![]() ,
,![]() ,
,
![]() 是
是![]() 上的减函数,又
上的减函数,又![]() ,故1是
,故1是![]() 的唯一零点,
的唯一零点,
当![]() ,
,![]() ,
,![]() ,
,![]() 递增;
递增;
当![]() ,
,![]() ,
,![]() ,
,![]() 递减;
递减;
故当![]() 时,
时,![]() 取得极大值且为最大值
取得极大值且为最大值![]() ,所以
,所以![]() .
.
(2)![]() ,令
,令![]() ,
,
以下证明当![]() 时,
时,![]() 的最小值大于0.
的最小值大于0.
求导得![]() .
.
①当![]() 时,
时,![]() ,
,![]() ;
;
②当![]() 时,
时,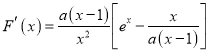 ,令
,令![]() .
.
则![]() ,又
,又![]() ,
,
取![]() 且使
且使![]() ,即
,即![]() ,则
,则![]() ,
,
因为![]() ,故
,故![]() 存在唯一零点
存在唯一零点![]() ,即
,即![]() 有唯一的极值点且为极小值点
有唯一的极值点且为极小值点![]() ,又
,又![]() ,且
,且![]() ,即
,即![]() ,
,
故![]() ,因为
,因为![]() ,故
,故![]() 是
是![]() 上的减函数.
上的减函数.
所以![]() ,所以
,所以![]() .
.
综上,当![]() 时,总有
时,总有![]() .
.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
【题目】有着“中国碳谷”之称的安徽省淮北市,名优特产众多,其中“塔山石榴”因其青皮软籽、籽粒饱满、晶莹剔透、汁多味甘而享誉天下.现调查表明,石榴的甜度与海拔、日照时长、昼夜温差有着极强的相关性,分别用![]() 表示石榴甜度与海拔、日照时长、温差的相关程度,并对它们进行量化:0表示一般,1表示良,2表示优,再用综合指标
表示石榴甜度与海拔、日照时长、温差的相关程度,并对它们进行量化:0表示一般,1表示良,2表示优,再用综合指标![]() 的值评定石榴的等级,若
的值评定石榴的等级,若![]() 则为一级;若
则为一级;若![]() 则为二级;若
则为二级;若![]() 则为三级.
则为三级.![]() 近年来,周边各地市也开始发展石榴的种植,为了了解目前石榴在周边地市的种植情况,研究人员从不同地市随机抽取了12个石榴种植园,得到如下结果:
近年来,周边各地市也开始发展石榴的种植,为了了解目前石榴在周边地市的种植情况,研究人员从不同地市随机抽取了12个石榴种植园,得到如下结果:
种植园编号 | A | B | C | D | E | F |
|
|
|
|
|
|
|
种植园编号 | G | H | I | J | K | L |
|
|
|
|
|
|
|
(1)若有石榴种植园120个,估计等级为一级的石榴种植园的数量;
(2)在所取样本的二级和三级石榴种植园中任取2个,![]() 表示取到三级石榴种植园的数量,求随机变量
表示取到三级石榴种植园的数量,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.