题目内容
【题目】已知函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]()
![]() ,
,![]() .
.
(1)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的极小值;
的极小值;
(3)若对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)求出![]() 在
在![]() 处的导数即得切线的斜率;求出切点坐标,根据点斜式方程求得切线方程;(2)讨论导函数的零点
处的导数即得切线的斜率;求出切点坐标,根据点斜式方程求得切线方程;(2)讨论导函数的零点![]() 与定义域的关系得到其单调性,找出极小值点,求得极小值;(3)对任意的
与定义域的关系得到其单调性,找出极小值点,求得极小值;(3)对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,等价于
成立,等价于![]() 在
在![]() 上的最小值大于
上的最小值大于![]() 在
在![]() 上的最小值,分别求出
上的最小值,分别求出![]() 的最小值和
的最小值和![]() 的最小值,得到
的最小值,得到![]() 的范围.
的范围.
试题解析:(1)因为![]() ,
,
所以![]() ,即切线的斜率为
,即切线的斜率为![]() .
.
又![]() ,则切点坐标为
,则切点坐标为![]() ,
,
故曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() .
.
(2)![]()
![]() ,
,
![]() ,又
,又![]() 的定义域
的定义域![]() ,
,
∴当![]() 时,令
时,令![]() ,
,![]() 或
或![]() ,
,
令![]() ,
,![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 单调递增,
单调递增,
∴![]() 的极小值为
的极小值为![]() ,
,
当![]() 时,
时,![]() ,
,
综上,![]() .
.
(3)对任意的![]() ,总存在
,总存在![]() ,
,
使得![]() 成立,等价于
成立,等价于![]() 在
在![]() 上的最小值大于
上的最小值大于![]() 在
在![]() 上的最小值,
上的最小值,
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上递减,
上递减,![]() ,
,
由(2)知,![]() 在
在![]() 上递增,
上递增,
![]() ,
,
∴![]() ,即
,即![]() ,又
,又![]() ,
,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
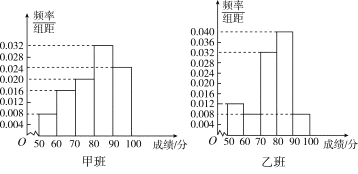
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
附:![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |