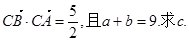题目内容
已知函数
(1)求函数 的值域,并写出函数
的值域,并写出函数 的单调递增区间;
的单调递增区间;
(2)若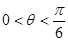 ,且
,且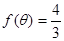 ,计算
,计算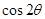 的值.
的值.
(1)值域为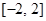 ;单调递增区间为
;单调递增区间为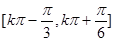 ,
, (2)
(2)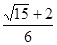 .
.
解析试题分析:(1)本小题首先需要对函数解析式进行化简变形得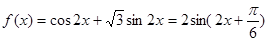 ,然后根据
,然后根据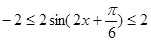 求得函数
求得函数 的值域为
的值域为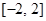 ;由
;由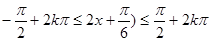 得
得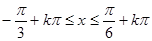 ,所以函数
,所以函数 的单调递增区间为
的单调递增区间为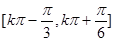 ,
, ;
;
(2)本小题首先根据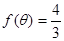 代入可得
代入可得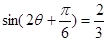 ,利用
,利用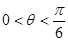 可判断
可判断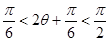 ,于是求得
,于是求得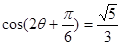 ,然后
,然后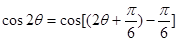 展开代入求值即可.
展开代入求值即可.
试题解析:(1)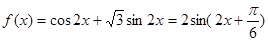 2分
2分
由于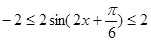 ,所以函数
,所以函数 的值域为
的值域为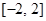 4分
4分
由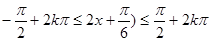 得
得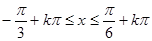
所以函数 的单调递增区间为
的单调递增区间为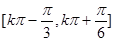 ,
, 6分
6分
(2)由(1)得,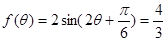 ,即
,即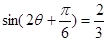 8分
8分
其中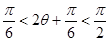 得
得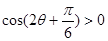 10分
10分
所以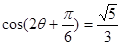 11分
11分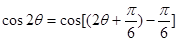 13分
13分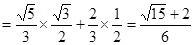 14分
14分
考点:1.三角恒等变换;2.正弦曲线的图像与性质.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
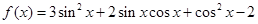 .
.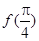 的值;
的值;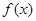 的最小正周期及单调递增区间.
的最小正周期及单调递增区间. ,
, .
. 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 中,若
中,若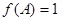 ,
,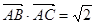 ,求△
,求△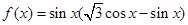
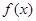 的单调增区间;(Ⅱ)当
的单调增区间;(Ⅱ)当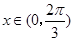 时,求
时,求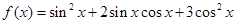 ,
,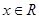 .求:
.求: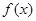 的最小值及取得最小值的自变量
的最小值及取得最小值的自变量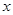 的集合;
的集合;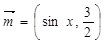 ,
,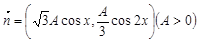 ,函数
,函数 的最大值为6.
的最大值为6. ;
;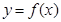 的图象向左平移
的图象向左平移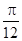 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的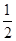 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数 的图象.求
的图象.求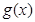 在
在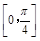 上的值域.
上的值域. 为坐标原点,
为坐标原点, ,
, .
.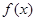 的定义域为
的定义域为 ,求
,求 的单调递增区间;
的单调递增区间; ,值域为
,值域为 ,求
,求 的值.
的值.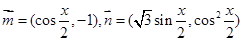 ,设函数
,设函数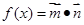 +
+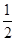
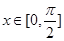 ,f(x)=
,f(x)=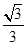 ,求
,求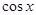 的值;
的值; 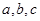 ,且满足
,且满足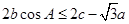 ,求f(B)的取值范围.
,求f(B)的取值范围. .
.