题目内容
已知向量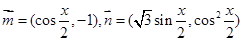 ,设函数
,设函数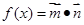 +
+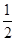
(1)若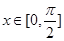 ,f(x)=
,f(x)=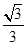 ,求
,求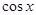 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是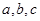 ,且满足
,且满足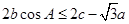 ,求f(B)的取值范围.
,求f(B)的取值范围.
(1)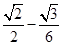 ;(2)
;(2)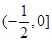
解析试题分析:(1)由向量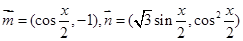 ,所以函数
,所以函数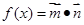 +
+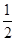 可求得
可求得 又有
又有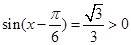 可求得
可求得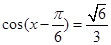 .再由
.再由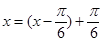 便可求得cosx的值.
便可求得cosx的值.
(2)由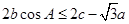 ,将边化角可得到
,将边化角可得到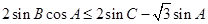 .即将sinC=sin(A+B)=sinAcosB+cosAsinB代入即可得到
.即将sinC=sin(A+B)=sinAcosB+cosAsinB代入即可得到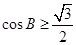 ,从而求出角B的范围.再求出sin(
,从而求出角B的范围.再求出sin(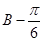 )
)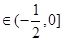
试题解析:(1)依题意得 , 2分
, 2分
由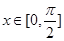 得:
得: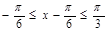 ,
,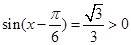 ,
,
从而可得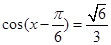 , 4分
, 4分
则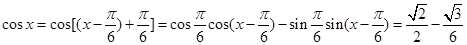 6分
6分
(2)由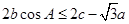 得:
得: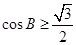 ,从而
,从而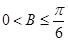 , 10分
, 10分
故f(B)=sin(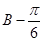 )
)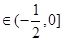 12分
12分
考点:1.向量的坐标形式的数量积.2.三角恒等变形.3.含三角的不等式的求法.4.三角形中两角和的正弦值等于另一个角的正弦值.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
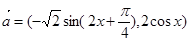 ,
,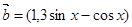 ,
,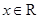 ,函数
,函数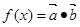 .
.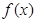 的最小正周期;
的最小正周期;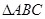 中,角
中,角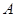 、
、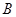 、
、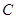 所对的边分别为
所对的边分别为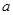 、
、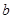 、
、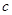 ,
,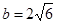 ,
, ,
,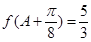 ,求
,求
 的值域,并写出函数
的值域,并写出函数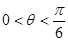 ,且
,且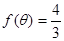 ,计算
,计算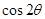 的值.
的值.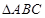 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为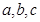 .
.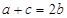 ,
,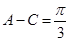 ,求
,求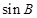 的值.
的值.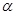 的顶点在原点,始边与
的顶点在原点,始边与 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点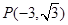 .
.  的值;
的值;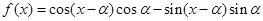 ,求函数
,求函数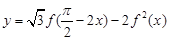 在区间
在区间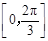 上的取值范围.
上的取值范围.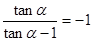 ,求下列各式的值:
,求下列各式的值: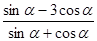 ;
;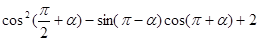 .
. ,
, ,函数
,函数 .将函数
.将函数 的图象上各点的纵坐标保持不变,横坐标先缩短到原来的
的图象上各点的纵坐标保持不变,横坐标先缩短到原来的 ,把所得到的图象再向左平移
,把所得到的图象再向左平移 个单位,得到函数
个单位,得到函数 的图象.
的图象. 的单调递增区间;
的单调递增区间; ,求
,求
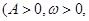
 的部分图象
的部分图象
 的解析式
的解析式  且
且 求
求 的值
的值  ,1),p=(
,1),p=( ,
, )且
)且 .
. 的值;
的值; 的取值范围?
的取值范围?