题目内容
 如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成角为
如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成角为| π | 3 |
(1)证明:点B1在平面ABC上的射影O为AB的中点;
(2)求二面角C-AB1-B的正切值;
(3)求点A1到平面CB1A的距离.
分析:(1)过B1点作B1O⊥BA,由面面垂直的性质,可得A1O⊥面ABC,即O为点B1在平面ABC上的射影,进而∠B1BA是侧棱BB1与底面ABC的夹角,由已知中侧棱BB1与底面ABC所成角为
,解Rt△BOB1,易得O是AB的中点.
(2)连接AB1,过点O作OM⊥AB1,连接CM,OC,可证得∠OMC是二面角C-AB1-B的平面角,解Rt△OMC,即可求出二面角C-AB1-B的正切值;
(3)方法一:过点O作ON⊥CM,可证得ON⊥面ACB1,即ON的长度是O点到平面ACB1DE距离,连接BA1与B1A交于H,则H是BA1的中点,即B与A1到平面ACB1的距离相等,结合(1)的结论,求出B到平面ACB1的距离,即可得到答案.
(3)方法二:根据VA1-ACB1=VC-AB1A1,分别求出三棱锥的体积和三角形ACB1的面积,即可得到答案.
| π |
| 3 |
(2)连接AB1,过点O作OM⊥AB1,连接CM,OC,可证得∠OMC是二面角C-AB1-B的平面角,解Rt△OMC,即可求出二面角C-AB1-B的正切值;
(3)方法一:过点O作ON⊥CM,可证得ON⊥面ACB1,即ON的长度是O点到平面ACB1DE距离,连接BA1与B1A交于H,则H是BA1的中点,即B与A1到平面ACB1的距离相等,结合(1)的结论,求出B到平面ACB1的距离,即可得到答案.
(3)方法二:根据VA1-ACB1=VC-AB1A1,分别求出三棱锥的体积和三角形ACB1的面积,即可得到答案.
解答: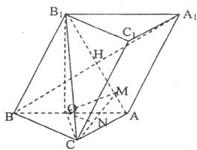 证明:(1)过B1点作B1O⊥BA.
证明:(1)过B1点作B1O⊥BA.
∵侧面ABB1A⊥底面ABC,∴A1O⊥面ABC
∴∠B1BA是侧棱BB1与底面ABC的夹角;
∴∠B1BO=60°;在Rt△BOB1中,BB1=2,∴BO=
BB1=1
又∵BB1=AB,∴OB=
AB,∴O是AB的中点
即点B1在平面ABC上的射影O为AB的中点;
解:(2)连接AB1,过点O作OM⊥AB1,连接CM,OC
∵OC⊥AB,平面ABC⊥面AA1BB1,
∴OM⊥AB1
∴AB1⊥CM,∴∠OMC是二面角C-AB1-B的平面角;
在Rt△OCM中,OC=
,OM=
,∴tan∠OMC=2
∴二面角C-AB1-B的正切值为2;
(3)方法一:
过点O作ON⊥CM,∵AB1⊥平面OCM,∴AB1⊥ON;
∴ON⊥面ACB1,∴ON的长度是O点到平面ACB1DE距离;
在Rt△OMC中,OC=
,OM=
,∴CM=
∴ON=
=
连接BA1与B1A交于H,则H是BA1的中点;
∴B与A1到平面ACB1的距离相等;
又∵O是AB的中点,∴B到平面AB1C的距离是O到平面AB1C距离的2倍;
故A1到平面AB1C的距离为
方法二:(体积法)
VA1-ACB1=VC-AB1A1?S△△ACB1•h=S△AB1A1•OC
又在△ACB1中,AC=AB1=2,B1C=
?S△ACB1=
•
=
∴
•h=
×22×
?h=
,
∴A1到平面AB1C的距离为
 证明:(1)过B1点作B1O⊥BA.
证明:(1)过B1点作B1O⊥BA.∵侧面ABB1A⊥底面ABC,∴A1O⊥面ABC
∴∠B1BA是侧棱BB1与底面ABC的夹角;
∴∠B1BO=60°;在Rt△BOB1中,BB1=2,∴BO=
| 1 |
| 2 |
又∵BB1=AB,∴OB=
| 1 |
| 2 |
即点B1在平面ABC上的射影O为AB的中点;
解:(2)连接AB1,过点O作OM⊥AB1,连接CM,OC
∵OC⊥AB,平面ABC⊥面AA1BB1,
∴OM⊥AB1
∴AB1⊥CM,∴∠OMC是二面角C-AB1-B的平面角;
在Rt△OCM中,OC=
| 3 |
| ||
| 2 |
∴二面角C-AB1-B的正切值为2;
(3)方法一:
过点O作ON⊥CM,∵AB1⊥平面OCM,∴AB1⊥ON;
∴ON⊥面ACB1,∴ON的长度是O点到平面ACB1DE距离;
在Rt△OMC中,OC=
| 3 |
| ||
| 2 |
| ||
| 2 |
∴ON=
| OM•OC |
| CM |
| ||
| 5 |
连接BA1与B1A交于H,则H是BA1的中点;
∴B与A1到平面ACB1的距离相等;
又∵O是AB的中点,∴B到平面AB1C的距离是O到平面AB1C距离的2倍;
故A1到平面AB1C的距离为
2
| ||
| 5 |
方法二:(体积法)
VA1-ACB1=VC-AB1A1?S△△ACB1•h=S△AB1A1•OC
又在△ACB1中,AC=AB1=2,B1C=
| 6 |
| 1 |
| 2 |
| 6 |
22-(
|
| ||
| 2 |
∴
| ||
| 2 |
| ||
| 4 |
| 3 |
2
| ||
| 5 |
∴A1到平面AB1C的距离为
| ||
| 2 |
点评:本题考查的知识点是二面角的平面角及求法,点到平面的距离计算,其中熟练掌握棱柱的结构特征,及线面垂直、线线垂直、面面垂直之间的相互转化,熟练掌握二面角的定义等基础知识点是解答本题的关键.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 (甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=
(甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC= 如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成的角为
如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成的角为 如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为
如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为 (2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且
(2011•孝感模拟)如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成的角为θ,且 (2012•梅州二模)如图,已知斜三棱柱ABC-A1B1C1中,点B1在底面ABC上的射影落在BC上,CA=CB=a,AB=
(2012•梅州二模)如图,已知斜三棱柱ABC-A1B1C1中,点B1在底面ABC上的射影落在BC上,CA=CB=a,AB=