题目内容
4.已知$\overrightarrow{a}$=($\sqrt{3}$sinωx,1),$\overrightarrow{b}$=(cosωx,0),ω>0,又函数f(x)=$\overrightarrow{a}$•($\overrightarrow{a}$-k$\overrightarrow{b}$)(k>0)是以$\frac{π}{2}$为最小正周期的周期函数.(1)求函数f(x)的值域;
(2)若函数f(x)的最大值为$\frac{5}{2}$+$\sqrt{3}$,是否存在正实数t,使得函数f(x)的图象能由函数g(x)=t$\overrightarrow{a}•\overrightarrow{b}$的图象按向量平移得到.
分析 (1)首先利用向量的数量积运算得到f(x) 解析式,然后变形,利用其周期得到ω的值,从而得到值域;
(2)首先得到g(x)的解析式,然后观察与f(x)的关系,分析是否存在t.
解答 解:(1)$\overrightarrow{a}$=($\sqrt{3}$sinωx,1),$\overrightarrow{b}$=(cosωx,0),ω>0,
又函数f(x)=$\overrightarrow{a}$•($\overrightarrow{a}$-k$\overrightarrow{b}$)=3sin2ωx+1-k$\sqrt{3}$sinωxcosωx
=3×$\frac{1-cos2ωx}{2}$+1-$\frac{\sqrt{3}}{2}$ksin2ωx
=$\frac{5}{2}$-$\frac{3}{2}$cos2ωx-$\frac{\sqrt{3}}{2}$ksin2ωx
又函数是以$\frac{π}{2}$为最小正周期的周期函数,所以ω=2,
所以f(x)=$\frac{5}{2}$-$\frac{3}{2}$cos4x-$\frac{\sqrt{3}}{2}$ksin4x,
所以f(x)的值域为[$\frac{5}{2}$-$\sqrt{\frac{9+3{k}^{2}}{4}}$,$\frac{5}{2}$+$\sqrt{\frac{9+3{k}^{2}}{4}}$];
(2)若函数f(x)的最大值为 $\frac{5}{2}$+$\sqrt{3}$,即 $\frac{5}{2}$+$\sqrt{\frac{9+3{k}^{2}}{4}}$=$\frac{5}{2}$+$\sqrt{3}$,解得k=1,
所以f(x)=$\frac{5}{2}$-$\frac{3}{2}$cos4x-$\frac{\sqrt{3}}{2}$sin4x=$\frac{5}{2}$-$\sqrt{3}$sin(4x+$\frac{π}{3}$),
g(x)=t$\overrightarrow{a}•\overrightarrow{b}$=$\sqrt{3}$tsin2xcos2x=$\frac{\sqrt{3}t}{2}$sin4x,
所以当t=$\frac{2\sqrt{3}}{3}$时,g(x)=sin4x,只要将g(x)向左平移$\frac{π}{12}$个单位,然后纵坐标变为原来的$\sqrt{3}$倍,再将图象关于x轴对称,再向上平移$\frac{5}{2}$个单位即可得到f(x)图象.
点评 本题考查了向量的数量积运算以及三角函数图象的平移变换,考查了三角函数的周期性及其求法,属于基本知识的考查.

| A. | y=-$\frac{1}{2a}$ | B. | y=-$\frac{1}{4a}$ | C. | y=$\frac{1}{2a}$ | D. | y=$\frac{1}{4a}$ |
| A. | ?x≤0,lnx≥x | B. | ?x>0,lnx≥x | C. | ?x≤0,lnx<x | D. | ?x>0,lnx<x |
| A. | $\frac{4}{9}$ | B. | -$\frac{4}{9}$ | C. | $\frac{9}{4}$ | D. | -$\frac{9}{4}$ |
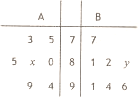 某学校从A、B两个班级中各选出7名学生参加市级比赛,他们去得的成绩(满分100分)的茎叶如图所示,其中A班学生成绩的众数是85,B班学生成绩的中位数是83.则x+y的值为8.
某学校从A、B两个班级中各选出7名学生参加市级比赛,他们去得的成绩(满分100分)的茎叶如图所示,其中A班学生成绩的众数是85,B班学生成绩的中位数是83.则x+y的值为8.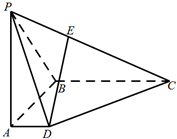 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.