题目内容
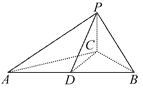
【题目】在如图所示的多面体中, ![]() 平面
平面![]() ,
, ![]() .
.
(1)在![]() 上求作点
上求作点![]() ,使
,使![]() 平面
平面![]() ,请写出作法并说明理由;
,请写出作法并说明理由;
(2)求三棱锥![]() 的高.
的高.
【答案】(1)详见解析(2)![]() .
.
【解析】试题分析:(1)由题意![]() ,因此只需
,因此只需![]() ,就可推出
,就可推出![]() 平面
平面![]() ,而
,而![]() 延长线与
延长线与![]() 交点恰为
交点恰为![]() 的中点
的中点![]() 因此作法为先取
因此作法为先取![]() 的中点
的中点![]() ,再连结
,再连结![]() ,交
,交![]() 于
于![]() .证法为先由线线平行证得线面平行,再由线面平行证得面面平行,最后由面面平行证得线面平行.(2)求三棱锥的高,可由等体积法求得:因为
.证法为先由线线平行证得线面平行,再由线面平行证得面面平行,最后由面面平行证得线面平行.(2)求三棱锥的高,可由等体积法求得:因为![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() ,这样只需求出两个三角形面积,代入化简即得三棱锥的高.
,这样只需求出两个三角形面积,代入化简即得三棱锥的高.
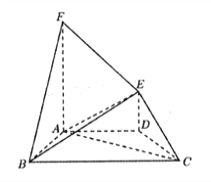
试题分析:解:(1)取![]() 的中点
的中点![]() ,连结
,连结![]() ,交
,交![]() 于
于![]() ,连结
,连结![]() .此时
.此时![]() 为所求作的点.
为所求作的点.
下面给出证明:
∵![]() ,∴
,∴![]() ,又
,又![]() ,∴四边形
,∴四边形![]() 是平行四边形,
是平行四边形,
故![]() 即
即![]() .
.
又![]() 平面
平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ;
;
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)在等腰梯形![]() 中,∵
中,∵![]() ,
,
∴可求得梯形的高为![]() ,从而
,从而![]() 的面积为
的面积为![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() 是三棱锥
是三棱锥![]() 的高.
的高.
设三棱锥![]() 的高为
的高为![]() .
.
由![]() ,可得
,可得![]() ,
,
即![]() ,解得
,解得![]() ,
,
故三棱锥![]() 的高为
的高为![]() .
.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求y关于x的线性回归方程。
(3)如果广告费支出为一千万元,预测销售额大约为多少百万元?
参考公式
用最小二乘法求线性回归方程系数公式: ,
, ![]() .
.
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下表所示:
零件的个数x/个 | 2 | 3 | 4 | 5 |
加工的时间y/h | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间.
【题目】某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意度进行调查,并随机抽取了其中30名员工(其中16名女员工,14名男员工)的得分,如下表:
女 | 47 36 32 48 34 44 43 47 46 41 43 42 50 43 35 49 |
男 | 37 35 34 43 46 36 38 40 39 32 48 33 40 34 |
(Ⅰ)现求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:
“满意”的人数 | “不满意”的人数 | 合计 | |
女 | 16 | ||
男 | 14 | ||
合计 | 30 |
(Ⅱ)根据上述表中数据,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关?
参考数据:
| 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考公式:![]()