题目内容
15.求函数y=-2sinx取最大值时的自变量x的集合.分析 由条件利用正弦函数的定义域和值域求得函数y取最大值时的自变量x的集合.
解答 解:函数y=-2sinx的最大值为2,此时,sinx=-1,x=2kπ-$\frac{π}{2}$,k∈z,
故函数取得最大值时的自变量x的集合为{x|x=2kπ-$\frac{π}{2}$,k∈z}.
点评 本题主要考查正弦函数的定义域和值域,属于基础题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
5. 如图,以Ox为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P,Q,已知点P的坐标为(-$\frac{3}{5},\frac{4}{5}$),β=30°,则sin(α-β)=( )
如图,以Ox为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P,Q,已知点P的坐标为(-$\frac{3}{5},\frac{4}{5}$),β=30°,则sin(α-β)=( )
 如图,以Ox为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P,Q,已知点P的坐标为(-$\frac{3}{5},\frac{4}{5}$),β=30°,则sin(α-β)=( )
如图,以Ox为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P,Q,已知点P的坐标为(-$\frac{3}{5},\frac{4}{5}$),β=30°,则sin(α-β)=( )| A. | $\frac{4+3\sqrt{3}}{10}$ | B. | $\frac{4\sqrt{3}+3}{10}$ | C. | $\frac{4-3\sqrt{3}}{10}$ | D. | $\frac{4\sqrt{3}-3}{10}$ |
6.若圆x2+y2-4x+2y+m+6=0与y轴的两交点A,B位于原点的同侧,则实数m的取值范围是( )
| A. | m<-1 | B. | m>-6 | C. | -6<m<-5 | D. | m<-5 |
20.已知集合M={x|x>$\frac{1}{x}$},N={x|y=$\frac{1}{\sqrt{1-lnx}}$},则M∩N=( )
| A. | (1,e) | B. | (0,1) | C. | (1,e] | D. | (e,+∞) |
4.$\underset{lim}{x→0}$$\frac{{∫}_{0}^{x}ln(cost)dt}{{x}^{3}}$=( )
| A. | 0 | B. | $\frac{1}{6}$ | C. | -$\frac{1}{6}$ | D. | ∞ |
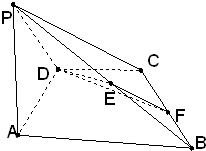 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD⊥DC,DC∥AB,PA=AB=2,AD=DC=1.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD⊥DC,DC∥AB,PA=AB=2,AD=DC=1.