题目内容
4.在各项均不为零的等差数列{an}中,若${a_n}^2={a_{n+1}}+{a_{n-1}}(n≥2,n∈N)$,则$S_{2015}^{\;}$等于( )| A. | 4030 | B. | 2015 | C. | -2015 | D. | -4030 |
分析 通过等差中项的性质可得2an=an-1+an+1,同时利用${a_n}^2={a_{n+1}}+{a_{n-1}}(n≥2,n∈N)$,结合题意即得等差数列{an}为常数列,进而可得结论.
解答 解:∵数列{an}为等差数列,
∴2an=an-1+an+1,
又∵${a_n}^2={a_{n+1}}+{a_{n-1}}(n≥2,n∈N)$,
∴2an=${{a}_{n}}^{2}$,
解得:an=2或an=0,
又∵数列{an}中各项均不为0,
∴an=2,
即等差数列{an}为常数列,
∴$S_{2015}^{\;}$=2015×2=4030,
故选:A.
点评 本题考查等差数列的性质,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
15.关于x的方程x2-2x+5=0的一个根是1-2i,则另一根的虚部为( )
| A. | 2i | B. | -2i | C. | 2 | D. | -2 |
9.已知向量$\vec a$=(1,n),$\vec b$=(-1,n),$\vec a$垂直于$\vec b$,则|${\vec a}$|=( )
| A. | 1 | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | 4 |
16.运行如图所示的程序框图,则输出k的值是( )
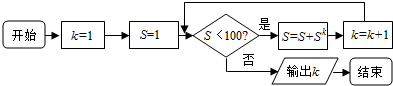

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
13.有4部车床需加工3个不同的零件,不同的安排方法有多少种?( )
| A. | 34 | B. | 43 | C. | 13 | D. | 14 |