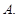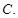题目内容
若函数 (常数
(常数 )是偶函数,且它的值域为
)是偶函数,且它的值域为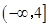 ,则该函数的解析式
,则该函数的解析式 .
.
 (常数
(常数 )是偶函数,且它的值域为
)是偶函数,且它的值域为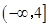 ,则该函数的解析式
,则该函数的解析式 .
.
解:∵f(x)=(x+a)(bx+2a)是偶函数,∴f(-x)=(-x+a)(-bx+2a)=f(x)=(x+a)(bx+2a),∴bx2-2ax-abx+2a2=bx2+2ax+abx+2a2,∴2ax+abx=0,即ax(2+b)=0恒成立,∴a=0或2+b=0.若a=0,则f(x)=bx2,若b>0,值域是y≥0,b<0,值域是y≤0,都不是(-∞,4],所以a≠0,故b+2=0,∴b=-2,所以f(x)=-2x2+2a2,∵-2x2≤0,所以值域是f(x)≤2a2,∴2a2=4,即f(x)=-2x2+4.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 ,
, 、
、 、
、 、
、 的值;
的值; 与
与 之间的等式关系,并证明这个等式关系;
之间的等式关系,并证明这个等式关系; 的值.
的值. 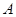 到
到 的映射
的映射 ,那么集合
,那么集合 ,其导函数为
,其导函数为 .
. 的单调减区间是
的单调减区间是 ;
; ;
; 时,对任意的
时,对任意的 且
且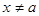 ,恒有
,恒有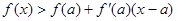

 ,
,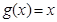
 ,
,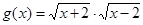
 ,
,
 ,
,

 :
: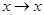 的平方根。
的平方根。
 。
。 :
: 中的数平方。
中的数平方。 的映射的是:
的映射的是:  地和
地和 地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知
地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知 米.(汽车开到
米.(汽车开到 秒后,汽车到达
秒后,汽车到达 处,自行车到达
处,自行车到达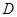 处,设
处,设 间距离为
间距离为 ,试写出
,试写出
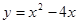 (
( )的值域为( )
)的值域为( )