题目内容
7.△ABC中,sinA:sinB:sinC=2:$\sqrt{6}$:($\sqrt{3}$+1),则三角形的最小内角是( )| A. | 60° | B. | 45° | C. | 30° | D. | 以上答案都不对 |
分析 已知等式利用正弦定理化简,求出三边之比,判断得到最小内角,利用余弦定理求出最小内角的余弦值,即可确定出最小内角.
解答 解:∵△ABC中,sinA:sinB:sinC=2:$\sqrt{6}$:($\sqrt{3}$+1),
∴由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$化简得:a:b:c=2:$\sqrt{6}$:($\sqrt{3}$+1),
设a=2k,b=$\sqrt{6}$k,c=($\sqrt{3}$+1)k,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{6{k}^{2}+(\sqrt{3}+1)^{2}{k}^{2}-4{k}^{2}}{2\sqrt{6}(\sqrt{3}+1){k}^{2}}$=$\frac{\sqrt{2}}{2}$,即A=45°,
则三角形的最小内角是45°,
故选:B.
点评 此题考查了正弦、余弦定理,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
18.如图是高尔顿板的改造装置,当小球从B自由下落时,进入槽口A处的概率为( )


| A. | $\frac{3}{16}$ | B. | $\frac{5}{16}$ | C. | $\frac{3}{32}$ | D. | $\frac{5}{32}$ |
16.设某几何体的三视图如图,则该几何体的体积为( )
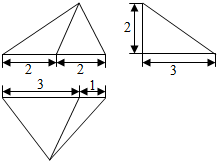

| A. | 12 | B. | 8 | C. | 4 | D. | 2 |
17.点A(sinα,cosα)在第二象限,则角α在直角坐标平面上位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
