题目内容
16.设某几何体的三视图如图,则该几何体的体积为( )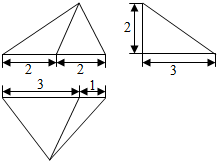
| A. | 12 | B. | 8 | C. | 4 | D. | 2 |
分析 根据几何体的三视图,得出该几何体是高为2的三棱锥,结合图中数据求出该三棱锥的体积.
解答 解:根据几何体的三视图,得;
该几何体是高为2的三棱锥,
且底面三角形的底边长为4,高为3;
所以该几何体的体积为
V三棱锥=$\frac{1}{3}$×($\frac{1}{2}$×4×3)×2=4.
故选:C.
点评 本题考查了空间几何体三视图的应用问题,解题的关键是根据三视图得出几何体的结构特征,是基础题目.

练习册系列答案
相关题目
7.△ABC中,sinA:sinB:sinC=2:$\sqrt{6}$:($\sqrt{3}$+1),则三角形的最小内角是( )
| A. | 60° | B. | 45° | C. | 30° | D. | 以上答案都不对 |
4.设a>b,c>d,则有( )
| A. | a-c>b-d | B. | ac>bd | C. | $\frac{a}{c}>\frac{d}{b}$ | D. | a+c>b+d |
11.函数f(x)=2x3-9x2+12x+1的单调递增区间( )
| A. | (1,2) | B. | (2,+∞) | C. | (-∞,1) | D. | (-∞,1)和(2,+∞) |
1.若G(x)=ax2+bx+3a+b是定义在[a-3,2a]上的偶函数,则a,b的值( )
| A. | a=0,b=1 | B. | a=1,b=0 | C. | a=b=0 | D. | a=b=1 |
8.sin$\frac{23π}{6}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |